Đề kiểm tra 15 phút - Đề số 5 - Bài 8 - Chương 2 - Hình học 9
Tóm tắt bài
Đề bài
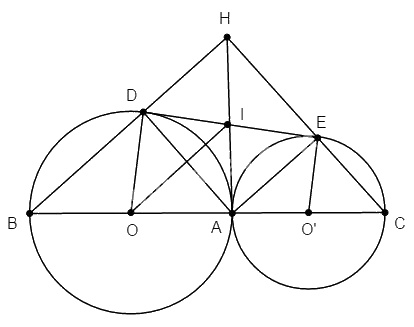
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Đường thẳng OO’ cắt (O) và (O’) lần lượt tại B và C (khác A). Gọi DE là tiếp tuyến chung ngoài của (O) và (O’). Trong đó, \(D ∈ (O), E ∈ (O’)\). Gọi H là giao điểm của hai đường thẳng BD và CE. Chứng minh rằng :
a. \(\widehat {DHE} = 90^\circ \)
b. HA là tiếp tuyến chung của hai đường tròn (O) và (O’).
Hướng dẫn giải
a. DE là tiếp tuyến chung ngoài của (O) và (O’) nên \(DE ⊥ OD\).
và \(DE ⊥ O’E ⇒ OD // O’E.\)
Do đó: \(\widehat {DOO'} + \widehat {EO'O} = 180^\circ \) (cặp góc trong cùng phía)
\( \Rightarrow \widehat {DOB} + \widehat {EO'C} = 180^\circ \)
Các tam giác BOD và CO’E cân tại O và O’ nên:
\(2\widehat B + 2\widehat C = 180^\circ \)
\(\Rightarrow 2\left( {\widehat B + \widehat C} \right) = 180^\circ \Rightarrow \widehat B + \widehat C = 90^\circ \)
Trong tam giác BHC ta có \(\widehat {BHC} = 90^\circ \,\,hay\,\,\widehat {DHE} = 90^\circ .\)
b. Dễ thấy tứ giác HDAE là hình chữ nhật (có ba góc vuông).
Gọi I là giao điểm hai đường chéo AH và DE, ta có \(ID = IA\) ( tính chất hai đường chéo hình chữ nhật).
Các tam giác ODI và OAI có : OI chung, \(DI = AI\) (cmt), \(OD = OA (=R)\)
Vậy \(∆ODI = ∆OAI\) (c.c.c)
\( \Rightarrow \widehat {OAI} = \widehat {ODI} = 90^\circ \) hay \(IA ⊥ BC\) tại A
\(⇒ HA\) là tiếp tuyến chung của (O) và (O’)
Copyright © 2021 HOCTAP247
