Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
Đề kiểm tra 15 phút - Đề số 9 - Bài 8 - Chương 2 - Hình học 9
Đề kiểm tra 15 phút - Đề số 9 - Bài 8 - Chương 2 - Hình học 9
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho đường tròn (O) đường kính BC. Một dây AD vuông góc với BC tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I) và (K) lần lượt là các đường tròn ngoại tiếp các tam giác HBE và HCF.
a. Xác định vị trí tương đối của đường tròn (I) và (O); (K) và (O); (I) và (K).
b. Chứng minh tứ giác AEHF là hình chữ nhật.
Hướng dẫn giải
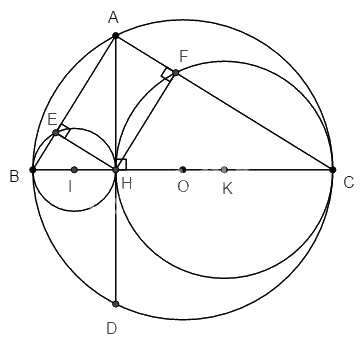
a. Ta có: \(OI = OB - IB\) (d = R – R1)
\(⇒ (I)\) và \((O)\) tiếp xúc trong.
Tương tự ta chứng minh được (K) và (O) tiếp xúc trong với nhau.
Lại có: \(IK = IH + HK\) (d = R1 + R2)
\(⇒ (I)\) và \((K)\) tiếp xúc ngoài với nhau.
b. Ta có: A thuộc đường tròn đường kính BC nên \(\widehat {BAC} = 90^\circ \) . Do đó AEHF là hình chữ nhật (có ba góc vuông).
Copyright © 2021 HOCTAP247
