Đề kiểm tra 15 phút - Đề số 10 - Bài 8 - Chương 2 - Hình học 9

Đề bài

Cho đường tròn tâm K có đường kính BC. Gọi D là trung điểm của KC và I là tâm của đường tròn có đường kính BD.

a. Chứng tỏ hai đường tròn (K) và (I) tiếp xúc trong với nhau.

b. Qua B vẽ đường thẳng (không trùng với BC) cắt (K) và (I) lần lượt tại A và E. Chứng tỏ KA // IE và \({{CA} \over {DE}}\) không đổi.

Hướng dẫn giải

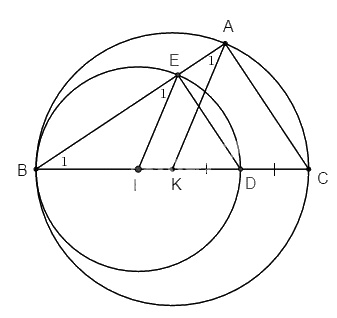
a. Ta có: \(IK = KB - IB \;(d = R - R’)\)

\(⇒\) Đường tròn (I) và (K) tiếp xúc trong với nhau.

b. Ta có: \(IB = IE\; (= R’)\) nên ∆BIE cân tại I \( \Rightarrow {\widehat B_1} = {\widehat E_1}\)

Tương tự ∆BKA cân tại K \( \Rightarrow {\widehat B_1} = {\widehat A_1}\)

Do đó: \({\widehat E_1} = {\widehat A_1}\) \(⇒\) AK // IE (cặp góc đồng vị)

Ta có: \(\widehat {BED} = \widehat {BAC} = 90^\circ \) \(⇒\) DE // AC

Theo Định lí Ta-lét, ta có: \({{CA} \over {DE}} = {{BC} \over {BD}}\) không đổi.