Giải bài 39 trang 123 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, Kẻ tiếp tuyến chung ngoài BC, B ϵ (O), C ϵ (O'). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
a) Chứng minh rằng ∠BAC = 90o
b) Tính số đo góc OIO'
c) Tính độ dài BC, biết OA = 9cm, O'A = 4cm.
Hướng dẫn giải
a) Áp dụng tính chất của hai tiếp tuyến cắt nhau, ta có:
\(IA= IB=IC \Rightarrow \Delta ABC \) vuông tại A \(\Rightarrow \widehat{BAC} = 90^0\)
b) Áp dụng tính chất của hai tiếp tuyến cắt nhau, ta có \(OI , O'I \) theo thứ tự là tia phân giác của \(\widehat{AIB} \ và\ \widehat{AIC}\)
\( \Rightarrow \widehat{OIO'}=90 ^0\) ( tính chất của hai tia phân giác của hai góc bù nhau).
c) Áp dụng hệ thức \(h^2= b'.c'\) vào tam giác vuông OIO', ta được:
\(IA^2 = OA.O'A = 36 \Rightarrow IA= 6(cm) \Rightarrow BC= 2IA = 12(cm)\)
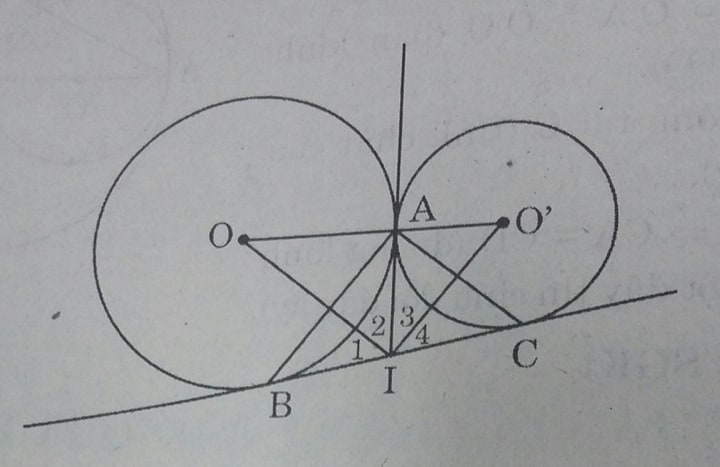
Copyright © 2021 HOCTAP247
