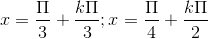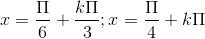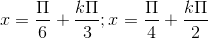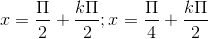Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Sử dụng công thức nhân, hạ bậc trong giải phương trình lượng giác có lời giải chi tiết
Sử dụng công thức nhân, hạ bậc trong giải phương trình lượng giác có lời giải chi tiết
Câu 2 : Giải phương trình: \(\cos x + 2{\cos ^2}{x \over 3} - 3 = 0\).
A \(x = k\pi \)
B \(x =6 k\pi \)
C \(x = {{k\pi } \over 2}\)
D \(x = {\pi \over 4} + k2\pi \)
Câu 3 : Giải phương trình \({\sin ^2}x = \sin 3x + \cos x\left( {\cos x - 1} \right)\)
A \(x = \frac{\pi }{4} + k\pi;\,\,x = - \frac{\pi }{2} + k2\pi ;\,\,x = \frac{{2k\pi }}{3}\,\,\left( {k \in Z} \right)\)
B \(x = \frac{\pi }{4} + k\pi ;\,\,x = \frac{\pi }{2} + k\pi ;\,\,x = \frac{{2k\pi }}{3}\,\,\left( {k \in Z} \right)\)
C \(x = \frac{\pi }{3} + k\pi ;\,\,x = - \frac{\pi }{2} + k2\pi ;\,\,x = - \frac{{2k\pi }}{3}\,\,\left( {k \in Z} \right)\)
D \(x = \frac{\pi }{6} + k\pi ;\,\,x = - \frac{\pi }{2} + k\pi ;\,\,x = \frac{{2k\pi }}{3}\,\,\left( {k \in Z} \right)\)
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247