Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
100 câu trắc nghiệm Hàm số lượng giác nâng cao !!
Khẳng định nào sau đây là đúng ? y =...
Khẳng định nào sau đây là đúng ? y = |tan x| đồng biến trong [-pi/2;pi/2]
Câu hỏi :
Khẳng định nào sau đây là đúng ?
A. y = |tan x| đồng biến trong [;]
B. y = |tan x| là hàm số chẵn trên D = R\ { + kπ | k ∈ Z}
C. y = |tan x| có đồ thị đối xứng qua gốc tọa độ.
D. y = |tan x| luôn nghịch biến trong (;)
* Đáp án
B
* Hướng dẫn giải
Đáp án B
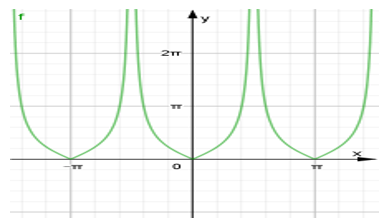
Ta được đồ thị như hình vẽ trên.
Ta thấy hàm số y = |tan x| nghịch biến trên (-π/2; 0) và đồng biến trên (0; π/2) . Nên ta loại A và D.
Với B ta có f(-x) = |tan(-x)| = | - tan x |= |tan x| = f(x) => hàm số y = |tan x| là hàm số chẵn.
Hàm số chẵn, nhận trục Oy làm trục đối xứng, không nhận tâm O làm tâm đối xứng.
Nên phương án C là sai
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
100 câu trắc nghiệm Hàm số lượng giác nâng cao !!
Số câu hỏi: 100
Copyright © 2021 HOCTAP247
