Cho phương trình: x^3 + 3x^2 - (24 + m)x - 26 - n = 0. Tìm

* Hướng dẫn giải

Chọn B

Vì ba nghiêm phân biệt $x_1,x_2,x_3$  lập thành một cấp số cộng nên ta đặt : $x_1=x_0-d,x_2=x_0,x_3=x_0+d(d\ne 0)$

Theo giả thiết Ta có: x3+3x2 – (24+m)x – 26- n= (x – x1)(x-x2)(x-x3)

=(x-xo+d)(x-xo)(x-xo-d)= x3 – 3xox2+ (3xo2-d2)x-xo3+ xod2 với mọi x.

Đồng nhất hai vế ta được:

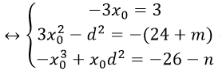
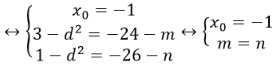
Vậy với m=n thì ba nghiệm phân biệt của phương trình lập thành một cấp số cộng