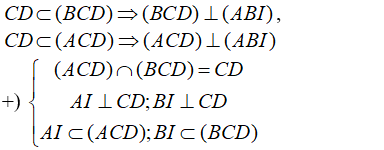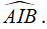Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Top 4 Đề kiểm tra 1 tiết Toán 11 Chương 3 Hình học có đáp án !!
Cho tứ diện ABCD có AC = AD và BC...
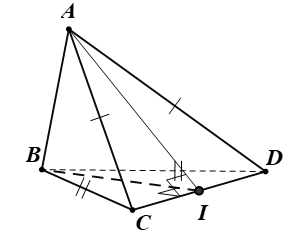
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD
Câu hỏi :
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là
C. (BCD) ⊥ (AIB).
D. (ACD) ⊥ (AIB).
* Đáp án
A
* Hướng dẫn giải
Chọn A.
+) Tam giác BCD có BC = BD nên cân tại B: Có BI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ BI (1)
+) Tam giác ACD có AC = AD nên cân tại A: Có AI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ AI (2)
- Từ (1) và (2) ⇒ CD ⊥ (ABI) (3)
+) Vì:
- Suy ra: góc giữa hai mặt phẳng (ACD) và (BCD) là
- Vậy: A sai.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 4 Đề kiểm tra 1 tiết Toán 11 Chương 3 Hình học có đáp án !!
Số câu hỏi: 47
Copyright © 2021 HOCTAP247