Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x^2 + y^2 + 2x - 6y + 6 = 0

* Hướng dẫn giải

Phép đối xứng tâm I(1; 2) biến đường  tròn (C) thành đường tròn  (C')

 và biến M(x; y) thuộc (C) thành M’(x’; y’) thuộc (C') thì:

(1)

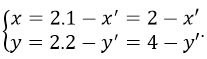
Vì điểm M(x, y) thuộc (C) nên: 

$x^2 +\hspace{0.17em} y^2+2x - 6y+\hspace{0.17em} 6 = 0$  (2) 

Thay (1) vào (2)  ta được:

${\left(2 - x\text{'}\right)}^2 + {\left(4 - y\text{'}\right)}^2 + 2(2 - x\text{'} ) - 6(4 - y\text{'} ) + 6 = 0$

⇒ $x{\text{'}}^2 + y{\text{'}}^2 - 6x\text{'} - 2y\text{'} + 6 = 0$

Suy ra phương trình (C')  $x^2 + y^2 - 6x - 2y + 6 = 0$

Đáp án A