Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Trắc nghiệm Đề kiểm tra Chương 2 Hình học 11 có đáp án !!
Cho hình chóp S.ABCD có đáy là hình bình hành....
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt
Câu hỏi :
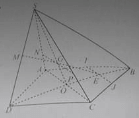
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. M là điểm thuộc cạnh SD. Khẳng định nào sau đây là đúng?
A. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC cắt nhau.
B. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC chéo nhau.
C. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng BD cắt nhau.
D. Giao tuyến của hai mặt phẳng (SAC) và (MIJ) và đường thẳng AC song song với nhau.
* Đáp án
D
* Hướng dẫn giải
Trong mặt phẳng (ABCD) ta có AC cắt BD tại O, IJ cắt BD tại E. trong mặt phẳng (SBD), ME cắt SO tại G. Ta có G thuộc (MIJ). (MIJ) chứa IJ // AC nên giao tuyến của (MIJ) với (SAC) là đường thẳng qua G và song song với AC.
Đáp án D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Đề kiểm tra Chương 2 Hình học 11 có đáp án !!
Số câu hỏi: 20
Copyright © 2021 HOCTAP247