Bài 25 trang 119 SGK Toán 9 tập 2

Đề bài

Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy \(a,b\) (\(a<b\)) và độ dài đường sinh là \(l\) (\(a,b,l\) có cùng đơn vị đo).

Hướng dẫn giải

+) Diện tích xung quanh hình nón: \(S_{xq}=\pi r l.\)

+) \(S_{xq \, \, nón \, \, cụt} = S_{xq \, \, hình \, \, nón \, \, lớn } - S_{xq \, \, hình \, \, nón \, \, nhỏ}.\)

Lời giải chi tiết

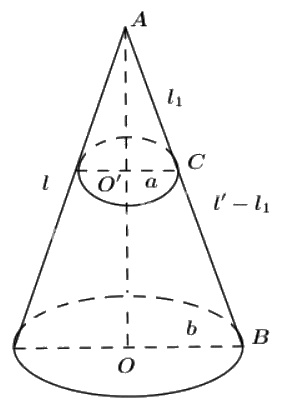
Kí hiệu như hình vẽ. Ta có hai tam giác vuông \(AO'C\) và \(AOB\) đồng dạng vì có góc chung.

 Nên \(\frac{l_1}{l - l_1}= \frac{a}b \Rightarrow l_1 = \frac{a}bl- \frac{a}bl_1\) 

 \(\Rightarrow (1+\frac {a}b)l_1 = \frac{a}{b}l \Rightarrow l_1 = \frac{a}{a+b}l\)

Diện tích xung quanh của hình nón lớn: 

\(S\)_{xq nón lớn}  \(= π.r.l =π.b.l\)

Diện tích xung quanh của hình nón nhỏ:

\(S\)_{xq nón nhỏ} =\(\pi .r.{l_1} = \pi .a.{a \over {a + b}}l = \pi {{{a^2}} \over {a + b}}l\)

Diện tích xung quanh của hình nón cụt là:

\(S\)_{xq nón cụt} =  \(S\)_{xq nón lớn} - \(S\)_{xq nón nhỏ}

\(= \pi b l - \pi \frac{a^2}{a +b}l=(b-\frac{a^2}{a+b})\pi l\)

\(= (\frac{b^2+ab- a^2}{a+b})\pi l.\)