Giải bài 28 trang 120 - Sách giáo khoa Toán 9 tập 2

Đề bài

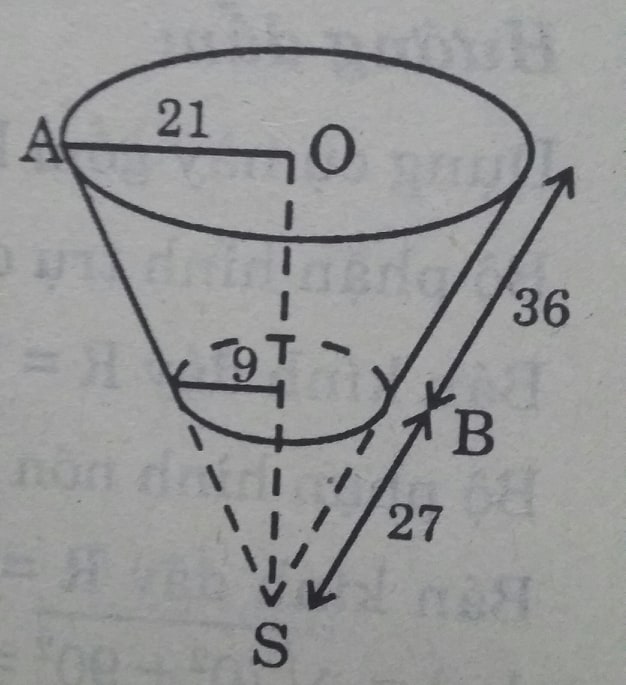
   Một cái xô bằng inox có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị: cm).

   a) Hãy tính diện tích xung quanh của xô.

   b) Khi xô chứa đầu hóa chất thì dung tích của nó là bao nhiêu?

Hướng dẫn giải

   a) Diện tích xung quanh của xô là:

   \(S_{xq} = \pi (R+r).l = \pi ( 21+9 ) .36= 1080 \pi (cm^2) \approx 3391,2 (cm^2)\)

   b) Để tính được dung tích của xô ta cần biết thêm chiều cao OO' của xô:

  Theo định lý Pitago ta có:

   \(SO = \sqrt{SA^2 - OA^2}= \sqrt{63^2-21^2 }= 42\sqrt{2}(cm)\\SO' = \sqrt{SB^2 - O'B^2}= \sqrt{27^2 - 9^2 }= 18\sqrt{2}(cm)\\ Vậy \ OO' = 42\sqrt{2}- 18\sqrt{2}= 24\sqrt{2}(cm) \approx 34(cm)\)

  Thể tích của xô là:  

   \(V = \dfrac{1}{3}\pi h (R^2 +r^2+R.r)\\V = \dfrac{1}{3}\pi.34( 21^2+9^2+21.9) \approx 25302 (cm^3) \ hay \ V \approx 25,3(l)\)