Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 2. Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Giải bài 17 trang 117 - Sách giáo khoa Toán 9 tập 2
Giải bài 17 trang 117 - Sách giáo khoa Toán 9 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Khi quay tam giác vuông để tạo ra một hình nón như hình thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là \(30^o\), độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Hướng dẫn giải
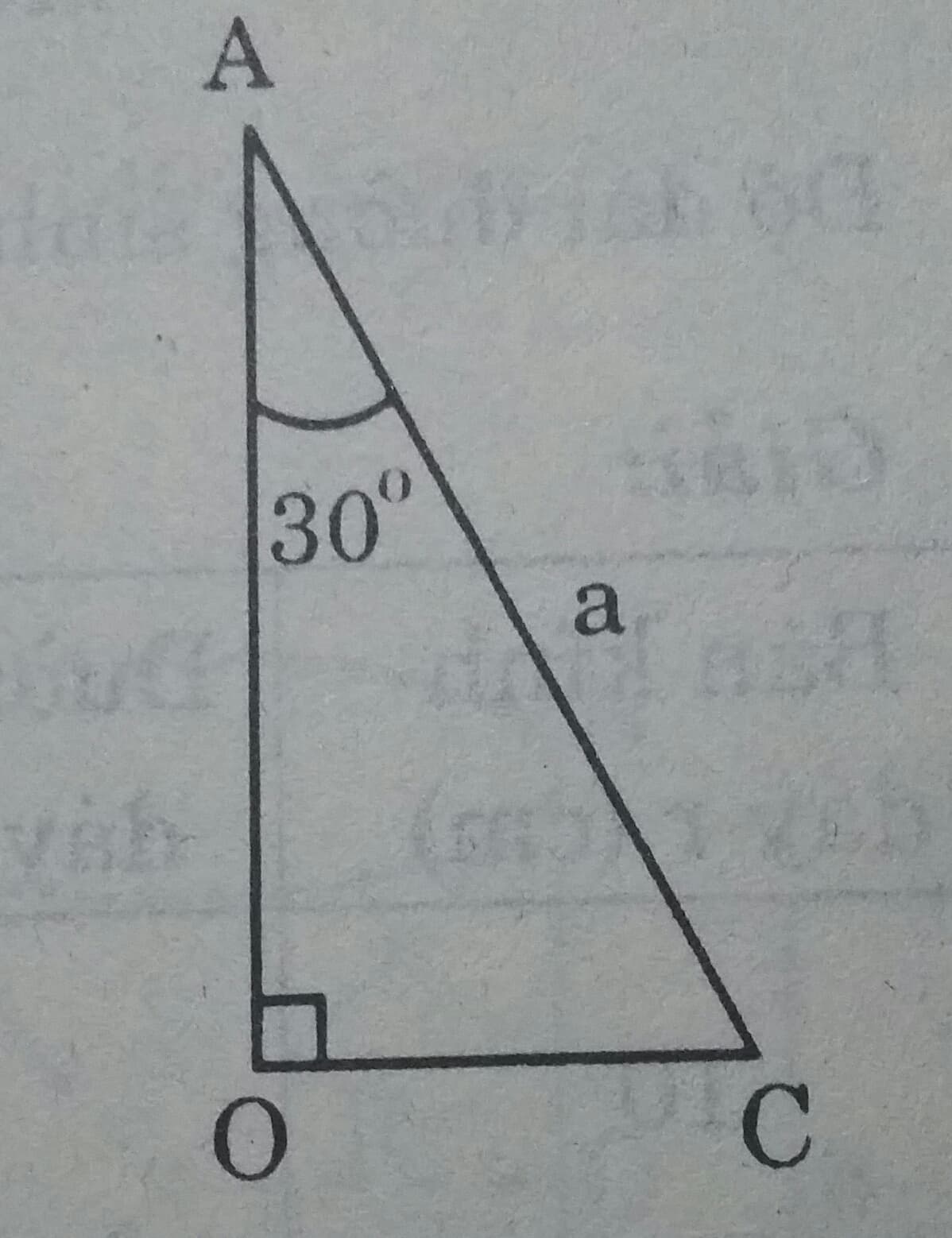
Bán kính đáy của hình nón là \(R = \dfrac{a}{2} \) ( Vì tam giác vuông CAO có \(\widehat{A}= 30^0\)).
Độ dài cung hình quạt khi khai triển mặt xung quanh của hình nón là:
\(l_1 = 2 \pi .\dfrac{a}{2}= \pi a.\)
Số đo cung của hình quạt là:
\(n = \dfrac{180.\pi.a}{\pi a }= 180 \)
Vậy số đo cung của hình quạt là \(180^0\)
Copyright © 2021 HOCTAP247
