Lý thuyết thể tích hình nón đầy đủ nhất

Ở trong bài viết này sẽ gửi đến các bạn lý thuyết về hình nón, thể tích hình nón đầy đủ nhất như: diện tích hình nón, thể tích hình nón cụt, các dạng bài tập về hình nón,... Các kiến thức trên hãy đi tìm hiểu ở trong bài viết này nhé!

A. Lý thuyết

I. Hình nón

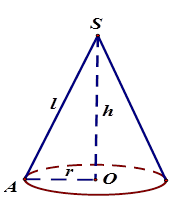
Cho hình nón có bán kính đáy R = OA, đường sinh \(l\) = SA, chiều cao h = SO. Vậy khi đó ta được:

- Diện tích hình nón:

• Diện tích xung quanh: \(S_{xq}=\pi Rl\)
• Diện tích đáy: \(S_{đ}=\pi R^2\)
• Diện tích toàn phần: \(S_tp = S_xq + S_đ = \pi Rl + \pi R^2\)

- Thể tích hình nón: V = \(\dfrac {1}{3}\pi R^2h\)

- Mở rộng: \(R^2 + h^2 = l^2\)

II. Hình nón cụt

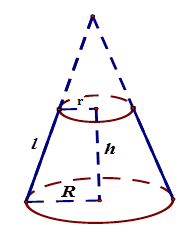
Cho hình nón cụt có bán kính đáy là R và r, h là chiều cao, \(l\) là đường sinh.

- Diện tích hình nón cụt:

• Diện tích xung quanh: \(S_{xq}=\pi (R + r)l\)
• Diện tích toàn phần: \(S_{tp} = \pi (R+r)l + \pi R^2 + \pi r^2\)

- Thể tích hình nón cụt: \(V = \dfrac {1}{3}\pi h (R^2 + Rr + r^2)\)

III. Các dạng bài tập về hình nón và hình nón cụt thường gặp

1. Dạng 1: Tính diện tích, thể tích và các đại lượng liên quan của hình nón.

=> Phương pháp: Áp dụng các công thức tính sau đây

- Diện tích hình nón:

• Diện tích xung quanh: \(S_{xq}=\pi Rl\)
• Diện tích đáy: \(S_{đ}=\pi R^2\)
• Diện tích toàn phần: \(S_tp = S_xq + S_đ = \pi Rl + \pi R^2\)

- Thể tích hình nón: V = \(\dfrac {1}{3}\pi R^2h\)

- Mở rộng: \(R^2 + h^2 = l^2\)

2. Dạng 2: Tính diện tích, thể tích và các đại lượng liên quan của hình nón cụt.

=> Phương pháp:

- Diện tích hình nón cụt:

• Diện tích xung quanh: \(S_{xq}=\pi (R + r)l\)
• Diện tích toàn phần: \(S_{tp} = \pi (R+r)l + \pi R^2 + \pi r^2\)

- Thể tích hình nón cụt: \(V = \dfrac {1}{3}\pi h (R^2 + Rr + r^2)\)

B. Bài tập hình nón có lời giải:

I. Bài tập tự luận

Bài 1: Cho một hình nón có bán kính đáy bằng 5cm, 65\(\pi \) (\(cm^2\)) là diện tích xung quanh của hình. Hỏi thể tích của hình nón đó bằng bao nhiêu?

=> Gợi ý đáp án: V = 100\(\pi \) (\(cm^3\)) 

Bài 2: Hãy tính chiều cao, diện tích toàn phần, thể tích của một hình nón khi được cho trước đường sinh bằng 15cm và diện tích xung quanh bằng 135\(\pi \) (\(cm^2\)) 

=> Gợi ý đáp án:

- h = 12(cm)

- Diện tích toàn phần là 216\(\pi \) (\(cm^2\)) 

- Thể tích hình nón 324\(\pi \) (\(cm^3\)) 

Bài 3: Nhà A sử dụng một chiếc xô hình nón được làm  bằng tôn đùng để đựng nước. Hình nón cụt đấy có bán kính đáy lần lượt bằng 14cm và 9cm, chiều cao h = 23cm.

a) Xô có dung tích bằng bao nhiêu?

b) Không kể diện tích các chỗ đã ghép hãy tính diện tích tôn được dùng để làm xô.

=> Gợi ý đáp án:

a) \(V = \dfrac {9296}{3}\pi (cm^3)\)

b) S = 612.5\(\pi \) (\(cm^2\))

Bài 4: Cho bán kính của một hình quạt bằng 20cm, có góc ở tâm bằng \(144^0\). Hãy tính số đo nửa góc ở đỉnh của hình nón này sau khi người ta đã uốn hình quạt này thành một hình nón.

=> Gợi ý đáp án: \(sin \alpha = 0,4\)

II. Bài tập trắc nghiệm

Câu 1: Công thức diện tích toàn phần \(S_{tp}\) nào dưới đây đúng? Trong đó cho biết trước hình nón có chiều cao h, \(l\) là độ dài đường sinh và r là bán kính đáy.

A. \(S_{tp}=\pi rl\)

B. \(S_{tp}=\pi rl+2\pi r\)

C. \(S_{tp}=\pi rl+\pi r^2\)

D. \(S_{tp}=2\pi rl + \pi r^2\)

=> Đáp án đúng: C

=> Lý giải chi tiết: \(S_{tp}=S_{xq}+S_đ=\pi rl + \pi r^2\)

Câu 2: Gọi độ dài đường sinh, chiều cao và bán kính của hình tròn đáy lần lượt là l, h, R. Hãy chọn một khẳng định đúng nhất dưới đây?

A. \(R^2 = h^2 + l^2\)

B. \( l^2 = h^2 + R^2\)

C. \(\dfrac {1}{l^2}=\dfrac {1}{h^2}+\dfrac {1}{R^2}\)

D. \(l^2 = h.R\)

=> Đáp án đúng: B

=> Lý giải chi tiết: Từ định lý Pi-ta-go trong tam giác vuông ta ABH ta có: \( l^2 = h^2 + R^2\)

Câu 3: Hình nón P được cho trước có chiều cao h = 4cm, bán kính đáy r = 3cm. Hãy tính diện tích xung quanh của hình nón (P)?

A. \(20\pi\)

B. \(15 \pi\)

C. \(10 \pi\)

D. \(5\pi\)

=> Đáp án đúng: B

=> Lý giải chi tiết: 

Do \(SHB\) là tam giác vuông, nên ta có có \(SB^2 = h = \sqrt{SH^2+HB^2} = \sqrt{4^2+3^2} = 5(cm)\)

Vậy: \(S_xq = \pi rl = \pi.3.5=15\pi (cm^2)\)

Câu 4: Hình nón P được cho trước có chiều cao h = 3cm, độ dài đường sinh l = 9cm. Hãy tính thể tích hình nón (P)?

A. 216\(\pi \) (\(cm^3\)) 

B. 12\(\pi \) (\(cm^3\)) 

C. \(\sqrt{72}\)\(\pi \) (\(cm^3\))

D. 27\(\pi \) (\(cm^3\))

=> Đáp án đung: C

=> Lý giải chi tiết: 

- Đề bài cho:

• Độ dài đường sinh l = SA = 9cm
• chiều cao h = SH = 3cm

- Tam giác SAH vuông nên ta có: AH = r = \(\sqrt{SA^2 - SH^2} = \sqrt{9^2 - 3^2} = \sqrt{72}\)

- Vậy thể tích của khối nón sẽ là: V = \(\dfrac {1}{3}\pi r^2 h = \dfrac {1}{3}\pi.72.3= 72\pi\) (\(cm^3\))

Câu 5: Quay tam giác đều ABC cạnh a xung quanh đường cao AH, tính diện tích của hình nón được sinh ra sau khi quay?

A. \(\pi a^2\)

B. \(2\pi a^2\)

C. \(\dfrac {\pi a^2}{2}\)

D. Một đáp án khác

=> Đáp án đúng: C

=> Lý giải chi tiết: 

- Dữ liệu đề bài cho: quay tam giác đều ABC cạnh a xung quanh đường cao AH thì ta sẽ được một hình nón có đỉnh là A và BC là đường tròn đường kính đáy.

- Theo tam giác đều đường cao đồng thời là đường trung tuyến ta có: BH = CH = \(\dfrac {1}{2}BC = \dfrac {1}{2}a = r\)

- Độ dài đường sinh l = AB = a

- Vậy diện tích xung quanh của hình nón trên sẽ là: \(S_{xq}=\pi rl = \pi \dfrac {a}{2}a=\dfrac {\pi. a^2}{2}\)

Câu 6: Cho trước hình nón có độ dài đường sinh bằng đường kính đáy bằng 2R. Hỏi diện tích xung quanh của hình nón đó sẽ bằng?

A. \(\pi R^2\)

B. \(2 \pi R^2\)

C. \(\dfrac {\pi R^2}{2}\)

D. \(4 \pi R ^2\)

=> Đáp án đúng: B

=> Lý giái chi tiết:

- Gọi độ dài đường kinh, bán kính đáy của hình nón lần lượt là l và r.

- Ta có: l = 2r = 2R => r = R

- Vậy diện tích xung quanh của hình nón đó sẽ là: \(S_{xq} = \pi rl = \pi R.2R = 2\pi R^2\)

Câu 7: Thể tích của khối nón sau khi quay tam giác ABC xung quanh cạnh AB, biết rằng tam giác này vuông cân tại đỉnh A, AB = 2a. Thể tích của khối nón bằng bao nhiêu?

A. \(3\pi a^2\)

B. \(\pi a^2\)

C. \(\dfrac {5}{3} \pi a^2\)

D. Một đáp án khác

=> Đáp án đúng: D

=> Lý giải chi tiết:

- Ta có:

• Độ dài đường cao h = AB = 2a
• Bán kính r = AC = 2a

- Vậy thể tích của khối nón sau khi quanh tam giác ABC quanh cạnh AB sẽ là: V = \(\dfrac {1}{3}\pi r^2 h = \dfrac {1}{3}(2a)^2.2a = \dfrac {8\pi a^3}{3}\) (\(cm^3\))

Câu 8: Quay tam giác ABC vuông tại B quanh cạnh AB. Hãy tính diện tích toàn phần của hình nón được tạo thành, biết AB = a, \(\widehat{A}=30^0\). 

A. \(3\pi a^2\)

B. \(\pi a^2\)

C. \(\dfrac {5}{3} \pi a^2\)

D. \(\sqrt{3}\pi a^2\)

=> Đáp án đúng: B

=> Lý giải chi tiết: 

- Vì tam giác ABC vuông tại B nên ta có: BC = AB.tan30 = a.\(\dfrac {1}{\sqrt{3}} = \dfrac {a}{\sqrt{3}} = r\)

- AC = \(\sqrt{AB^2 + BC^2} = \sqrt{a^2+\dfrac {a^2}{3}}= \dfrac {2a}{\sqrt{3}}=1\)

- Vậy diện tích toàn phần của tam giác ABC vuông tại B sau khi quanh cạnh AB là: \(S_{tp}=S_{xq}+ S_đ = \dfrac {2\pi a^2}{3}+ \dfrac {\pi a^2}{3}= \pi a^2\)

Câu 9: Hình chóp đều S,ABCD có đáy bằng 2a, cạnh bên bằng 3a. Hình nón (P) ngoại tiếp hình chóp đều S.ABCD. Tính thể tích của khối nón (P) vừa rồi.

A. \(\sqrt{7}\pi a^3 (cm^3)\)

B. \(\pi R^2 (cm^3)\)

C. \(2 \pi R^2 (cm^3)\)

D. Một đáp án khác

=> Đáp án đúng: D

=> Lý giải chi tiết:

- Khối nón ngoại tiếp hình chóp S.ABCD có đỉnh là S, có đáy nón là đường tròn ngoại tiếp hình vuông ABCD.

- Gọi giao điểm giữa AC và BD là O

Suy ra: SO vuông với (ABCD)

- Do ABCD là hình vuông có cạnh bằng 2a nên AC = BD = 2a\(\sqrt{2}\)

nên OA = \(\dfrac {1}{2}AC = a\sqrt{2} = r\)

- Xét tiếp tam giác vuông \(SOA \) ta có: \(SO = h = \sqrt{SA^2 - OA^2} = \sqrt{(3a)^2-(a\sqrt{2})^2} = a\sqrt{7}\)

- Vậy thể tích của khối nón (P) ngoại tiếp hình chóp đều S.ABCD sẽ bằng: \(V = \dfrac {1}{3}\pi r^2h = \dfrac {2\sqrt{7}\pi a^3}{3}(cm^3)\)

Câu 10: Cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng 23a. Hỏi diện tích xung quanh của hình nón vừa rồi bằng bao nhiêu?

A. \(6\pi a^2 (cm^2)\)

B. \(6\sqrt{2}\pi a^2 (cm^2)\)

C. \(\sqrt{2}\pi a^2 (cm^2)\)

D. \(3\sqrt{2}\pi a^2 (cm^2)\)

=> Đáp án đúng: D

=> Lời giải chi tiết:

- Diện tích tam giác ABC: \(S_{ABC}=\dfrac {1}{2}SA^2 = 3a^2\) => \(SA^2 = 6a^2 \Leftrightarrow SA = a\sqrt{6}=1\)

- Ta tính được AB = SA\(\sqrt{2}\) = 2a\(\sqrt{3}\)

                    => AI = \(\dfrac {1}{2}AB = a\sqrt{3} = r\)

- Diện tích xung quanh của hình nón sẽ bằng: \(S_{xq}= \pi rl = \pi a\sqrt{3}a\sqrt{6} = 3\sqrt{2}\pi a^2\)

Xem thêm >>> Giải bài tập toán 9 Hình nón hình nón cụt - SGK

Trên đây là toàn bộ những kiến thức lý thuyết về hình nón, thể tích hình nón, diện tích hình nón, thể tích hình nón cụt,...cùng các dạng bài tập về hình nón thường gặp mà muốn gửi đến cho các bạn học. Mong rằng với những kiến thức trên đây sẽ giúp ích được nhiều cho quá trình học tập của các bạn, chúc các bạn học tập tốt <3