Đề thi HK2 môn Toán lớp 11 Trường THPT Nguyễn Du - Phú Yên năm 2018
Câu 1 : Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x + 2}}.\)
A. 1
B. 2
C. 3
D. 4
Câu 2 : Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + \sqrt {{x^2} + 1} }}{{x + 2}}.\)
A. 1
B. 2
C. 3
D. 4
Câu 3 : Cho \(\mathop {\lim }\limits_{x \to 1} \frac{{x + \sqrt {{x^2} + 1} }}{{x + 1}} = a + b\sqrt 2 (a,b \in Q).\). Tính \(a+b\)
A. 1
B. 2
C. 5
D. 0
Câu 4 : Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + x - 2}}{{x - 1}}.\)
A. 1
B. - 2
C. 3
D. 5
Câu 5 : Tính giới hạn \(\mathop {\lim }\limits_{x\,\, \to \,\,2} (x - 2)\)
A. 7
B. - 2
C. 3
D. 0
Câu 6 : Biết \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x - m\sqrt {{x^2} + 2} }}{{x + 2}} = 2.\) Tìm m.
A. 1
B. - 2
C. 3
D. 4
Câu 7 :
Tìm m để hàm số \(y = \left\{ \begin{array}{l}
\frac{{{x^2} - 4}}{{x - 2}},\quad \quad x \ne 2\\
m,\quad \quad \quad \quad x = 2
\end{array} \right.\quad \) liên tục tại x = 2
A. 1
B. 2
C. 4
D. - 4
Câu 8 : Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {2x + 2} - 2x}}{{x - 1}}\)
A. \( - \frac{1}{2}.\)
B. 2
C. 3
D. \( - \frac{3}{2}.\)
Câu 9 : Biết \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m;\mathop {\lim }\limits_{x \to + \infty } g(x) = n.\) Tính \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) + g(x)} \right]\)
A. \(m+n\)
B. \(m-n\)
C. \(m\)
D. \(n\)
Câu 10 : Biết \(\mathop {\lim }\limits_{x \to 2} f(x) = 3.\) Tính \(\mathop {\lim }\limits_{x \to 2} \left[ {f(x) + x} \right].\)
A. 5
B. - 2
C. 1
D. 4
Câu 11 : Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{{{({x^2} + 2x - 2)}^5} - 1}}{{x - 1}}.\)
A. 1
B. 2
C. 3
D. 20
Câu 12 : Tính giới hạn \(\mathop {\lim }\limits_{} \frac{{n + 1}}{{{n^2} + 2}}.\)
A. 1
B. 2
C. 3
D. 0
Câu 13 : Tính giới hạn \(\mathop {\lim }\limits_{} \frac{{n + \sqrt {{n^2} + 1} }}{{n + 3}}.\)
A. 1
B. 2
C. 3
D. 4
Câu 14 : Cho dãy số \(u_n\) thỏa \(\mathop {\lim }\limits_{} {u_n} = 2.\) Tính \(\mathop {\lim }\limits_{} \left( {{u_n} + \frac{{{2^n}}}{{{2^n} + 3}}} \right).\)
A. 1
B. 2
C. 3
D. 4
Câu 15 : Cho dãy số \(u_n, v_n\) thỏa \(\mathop {\lim }\limits_{} {u_n} = 2,\mathop {\lim }\limits_{} {v_n} = 1.\) Tính \(\mathop {\lim }\limits_{} (2{u_n} - 3{v_n}).\)
A. 1
B. 2
C. 3
D. 7
Câu 16 : Tính đạo hàm của hàm số \(y = {x^2} + 1\)
A. \(y' = {x^2} + 1\)
B. \(y' = 2x + 1\)
C. \(y' = 2x\)
D. \(y' = 2x - 1\)
Câu 17 : Tính đạo hàm của hàm số \(y = \sin 2x\).
A. \(y' = 2\sin x\)
B. \(y' = \sin 2x\)
C. \(y' = 2\cos x\)
D. \(y' = 2\cos 2x\)
Câu 18 : Tính đạo hàm của hàm số \(y = {({x^2} + x)^2}\).
A. \(y' = 3{({x^2} + x)^2}\)
B. \(y' = 2x + 1\)
C. \(y' = 2(2x + 1)\)
D. \(y' = 2({x^2} + x)(2x + 1)\)
Câu 19 : Cho hàm số \(y = f(x) = {x^2} + mx\) (\(m\) là tham số) . Tìm \(m\), biết \(f'(1) = 3\).
A. \(m=1\)
B. \(m=2\)
C. \(m=3\)
D. \(m=7\)
Câu 20 : Cho hàm số \(y=\sin x\).Tính \(y''(0)\)
A. \(y''(0) = 0.\)
B. \(y''(0) = 1.\)
C. \(y''(0) = 2.\)
D. \(y''(0) = -2.\)
Câu 21 : Cho hàm số \(y=f(x)\) có đạo hàm trên tập số thực.Tìm hệ thức đúng?
A. \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}}.\)
B. \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{{x - 1}}.\)
C. \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{x}.\)
D. \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(1)}}{{x - 1}}.\)
Câu 22 : Cho hàm số \(y=f(x)\) có đạo hàm đến cấp 2 trên tập số thực.Tìm hệ thức đúng?
A. \(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}}.\)
B. \(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f'(x) - f'(1)}}{{x - 1}}.\)
C. \(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{x}.\)
D. \(f''(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(1)}}{{x - 1}}.\)
Câu 23 : Tìm hệ số của x trong khai triển \({({x^2} + x + 2)^2}(x + 1)\) thành đa thức
A. 16
B. 6
C. 8
D. 2
Câu 24 : Tìm hệ số của x2 trong khai triển \({({x^2} + x + 2)^3}\) thành đa thức
A. 12
B. 18
C. 19
D. 20
Câu 25 : Hàm số \(y = (1 + x)\sqrt {1 - x} \) có đạo hàm \(y' = \frac{{ax + b}}{{2\sqrt {1 - x} }}\).Tính \(a+b\)
A. - 2
B. 2
C. - 3
D. 1
Câu 26 : Lập phương trình tiếp tuyến của đồ thị hàm số \(y = {x^2} + 3x + 1\) tại điểm có hoành độ bằng 1.
A. y = 5x
B. y = 5x+5
C. y = 5x-5
D. y = x
Câu 27 : Hàm số \(y = \frac{{\sqrt {{x^2} + 2x + 3} }}{x}\) có đạo hàm \(y' = \frac{{ax + b}}{{{x^2}\sqrt {{x^2} + 2x + 3} }}\).Tìm \(\max \left\{ {a,b} \right\}.\)
A. 2
B. - 1
C. - 3
D. - 7
Câu 28 : Cho hàm số \(y=f(x)\) có đạo hàm trên tập số thực, biết \(f(3 - x) = {x^2} + x\).Tính \(f'(2)\)
A. \(f'(2) = - 1.\)
B. \(f'(2) = - 3.\)
C. \(f'(2) = - 2.\)
D. \(f'(2) = 3\)
Câu 29 : Tìm vi phân của hàm số \(y=x^3\)
A. \(dy = {x^2}dx.\)
B. \(dy = 3xdx.\)
C. \(dy = 3{x^2}dx.\)
D. \(dy = - 3{x^2}dx.\)
Câu 30 : Giải phương trình \(f''(x) = 0\), biết \(f(x) = {x^3} - 3{x^2}\).
A. x = 0
B. x = 2
C. x = 0, x = 2
D. x = 1
Câu 31 : Cho chuyển động thẳng xác định bởi phương trình \(s = {t^3} - 3{t^2} - 9t + 2\) ( t được tính bằng giây, s được tính bằng mét). Tìm gia tốc khi t = 2s.
A. \(a = 12m/{s^2}.\)
B. \(a = 6m/{s^2}.\)
C. \(a = -9m/{s^2}.\)
D. \(a = 2m/{s^2}.\)
Câu 32 : Tìm hệ số góc k của tiếp tuyến của đồ thị \(y = {x^3} - 2{x^2} - 3x + 1\) tại điểm có hoành độ bằng 0.
A. k = -3
B. k = 2
C. k = 1
D. k = 0
Câu 33 : Cho chuyển động thẳng xác định bởi phương trình \(s = {t^2} - 2t + 2\) ( t được tính bằng giây, s được tính bằng mét). Tính vận tốc tại thời điểm t = 3s.
A. \(v = 2m/s.\)
B. \(v = 4m/s.\)
C. \(v = -2m/s.\)
D. \(v = -4m/s.\)
Câu 34 : Tính \(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x).\)
A. \(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = xsinxdx.\)
B. \(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = x{\mathop{\rm cosxdx}\nolimits} .\)
C. \(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = {\mathop{\rm cosxdx}\nolimits} .\)
D. \(d({\mathop{\rm s}\nolimits} {\rm{inx}} - x\cos x) = sinxdx.\)
Câu 35 : Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên).Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
A. \(\frac{2}{3}.\)
B. \(\frac{1}{3}.\)
C. \(\frac{{\sqrt 3 }}{2}.\)
D. \(\frac{{\sqrt 2 }}{2}.\)
Câu 36 :
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC = 1. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng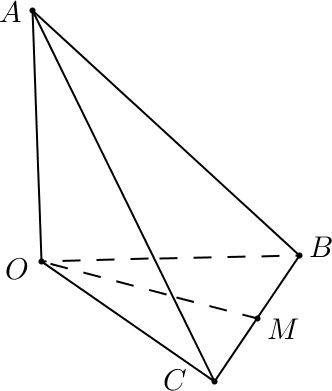
A. \(90^0\)
B. \(30^0\)
C. \(60^0\)
D. \(45^0\)
Câu 37 : Cho tứ diện đều ABCD. Tìm góc giữa hai đường thẳng AB và CD.
A. \(30^0\)
B. \(45^0\)
C. \(60^0\)
D. \(90^0\)
Câu 38 : Giải bất phương trình \(f'(x) > 0\), biết \(f(x) = 2x + \sqrt {1 - {x^2}} .\)
A. \(x \in \left( { - 1;\frac{1}{{\sqrt 2 }}} \right).\)
B. \(x \in \left( { - 1;1} \right).\)
C. \(x \in \left( { - 1;\frac{2}{{\sqrt 5 }}} \right).\)
D. \(x \in \left( { - \frac{2}{{\sqrt 5 }};\frac{2}{{\sqrt 5 }}} \right).\)
Câu 39 :
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a ( Tham khảo hình vẽ bên). Đường thẳng nào dưới đây vuông góc với mặt phẳng (ABCD) ?..png)
A. SD
B. SA
C. SB
D. SC
Câu 40 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Đường thẳng nào dưới đây vuông góc với mặt phẳng (SAB) ?
A. AB
B. AC
C. AD
D. AS
Câu 41 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Mặt phẳng nào dưới đây vuông góc với mặt phẳng (SAB) ?
A. (SAB)
B. (SAC)
C. (SAD)
D. (SCD)
Câu 42 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Khoảng cách từ S đến mặt phẳng (ABCD) bằng
A. SD
B. SA
C. SB
D. SC
Câu 43 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính tang của góc tạo bởi hai đường thẳng SB và CD
A. 3
B. \(\sqrt 2 .\)
C. \(\frac{{\sqrt 2 }}{3}.\)
D. 2
Câu 44 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách giữa hai đường thẳng SA và BC.
A. \(a\)
B. \(\sqrt 2 a.\)
C. \(2a\)
D. \(3a\)
Câu 45 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính tang của góc tạo bởi đường thẳng SC và mặt phẳng (ABCD)
A. 3
B. \(\sqrt 2 .\)
C. \(\frac{{\sqrt 2 }}{3}.\)
D. 2
Câu 46 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính côsin của góc tạo bởi mặt phẳng (SBD) và mặt phẳng (ABCD).
A. \(\frac{1}{3}.\)
B. 3
C. \(\sqrt 2 .\)
D. \(\frac{3}{{\sqrt 2 }}.\)
Câu 47 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách từ điểm D đến đường thẳng SB.
A. \(3a\)
B. \(\frac{3}{5}a.\)
C. \(\frac{{3\sqrt 5 }}{5}a.\)
D. \(\frac{{\sqrt {21} a}}{3}.\)
Câu 48 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Biết \(\overrightarrow {AC} = m\overrightarrow {AB} + n\overrightarrow {AD} + p\overrightarrow {AS} \). Tính tổng \(m+n+p\)
A. 3
B. 2
C. 1
D. 0
Câu 49 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
A. \(a\)
B. \(\sqrt 2 a.\)
C. \(\frac{{2\sqrt 5 }}{5}a.\)
D. \(\frac{{\sqrt {21} }}{3}a.\)
Câu 50 : Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng chứa đáy (ABCD), độ dài cạnh SA bằng 2a. Tính khoảng cách từ điểm A đến mặt phẳng (SBD).
A. \(2a\)
B. \(\sqrt 2 a.\)
C. \(\frac{2}{3}a.\)
D. \(\frac{3}{2}a.\)
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
