Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Bài tập Hình học không gian cơ bản, nâng cao có lời giải !!
Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường...
Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng
Câu hỏi :
Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng A'B với mặt phẳng (ABC) bằng và khoảng cách từ điểm A đến mặt phẳng (A'BC) bằng . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
* Đáp án
A
* Hướng dẫn giải
Đáp án A.
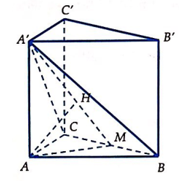
Gọi M là trung điểm của BC thì BC(A'AM)
Từ A kẻ AHA'M, ![]()
Suy ra
![]()
Góc giữa đường thẳng A'B và mặt phẳng (ABC) bằng góc
Theo giả thiết ta có =
Đặt AB = 2x ![]()
Từ giả thiết ta có
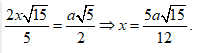
Do đó:
![]()
Vậy thể tích khối lăng trụ ABC.A'B'C' là
Phân tích phương án nhiễu.
Phương án B: Sai do HS tính đúng như trên nhưng nhớ nhầm công thức tính thể tích khối lăng trụ sang công thức tính thể tích khối chớp.
Cụ thể
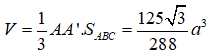
Phương án C: Sai do HS giải như trên và tìm được ![]() nhưng lại tính sai diện tích tam giác ABC. Cụ thể
nhưng lại tính sai diện tích tam giác ABC. Cụ thể
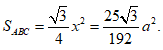
Do đó tính được
![]()
Phương án D: Sai do HS tính đúng như trên nhưng tính sai diện tích tam giác ABC. Cụ thể:
![]()
Do đó tính được
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hình học không gian cơ bản, nâng cao có lời giải !!
Số câu hỏi: 374
Copyright © 2021 HOCTAP247
