Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Bài tập Hình học không gian cơ bản, nâng cao có lời giải !!
Cho tấm tôn hình nón có bán kính đáy là...
Cho tấm tôn hình nón có bán kính đáy là r = 2/3, độ dài đường sinh
Câu hỏi :
Cho tấm tôn hình nón có bán kính đáy là r = , độ dài đường sinh l = 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khí cắt hình quạt theo hình chử nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
* Đáp án
B
* Hướng dẫn giải
Đáp án B.
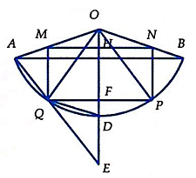
Qua O kẻ đường thẳng vuông góc với MN, đường thẳng này cắt MN, PQ, cung AB,AQ lần lượt tại
Độ dài cung AB là chu vi đường tròn đáy của hình nón nên
Lại có
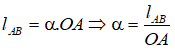
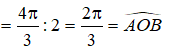
Áp dụng định lý cosin trong tam giác OAB có
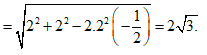
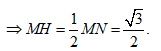
Do ODAB nên OD là tia phân giác của 
. Xét tam giác vuông OMH có OH =
Xét tam giác OPQ có
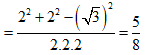
Mà
Xét tam giác DOQ có:
Xét tam giác vuông DQF có
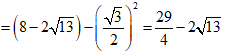
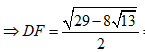
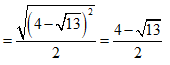
=> HF = OD - OH - DF =
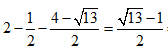
= MQ - NP
Gọi R là bán kính đáy của hình trụ tạo bởi hình chữ nhật MNPQ. Chu vi đáy của hình trụ chính là độ dài của PQ nên
Khi đó thể tích khối trụ tạo ra bởi hình chữ nhật MNPQ là:
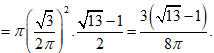
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hình học không gian cơ bản, nâng cao có lời giải !!
Số câu hỏi: 374
Copyright © 2021 HOCTAP247