Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải !!
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a...
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’
Câu hỏi :
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho . Mặt phẳng qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích . Tính tỉ số
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Gọi tâm O, O’ lần lượt là tâm của ABCD, A’B’C’D’. Ta có
![]()
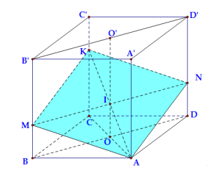
Qua I ta kẻ đường thẳng d song song BD cắt BB', DD' lần lượt tại M, N . Mặt phẳng chính là mặt phẳng (KMAN) chia khối lập phương thành 2 phần.
Ta có 2 phần khối đa diện đối xứng qua (AA'C'C) nên ta chỉ cần xét một nửa thể tích của mỗi phần như sau:
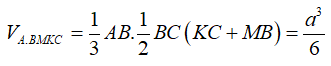
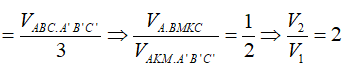
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải !!
Số câu hỏi: 181
Copyright © 2021 HOCTAP247
