Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD = a căn 2, AB =a

* Hướng dẫn giải

Đáp án D

nên $∆$BCDlà tam giác đều.

nên theo định lý Py-ta-go đảo, ta có $∆$ACD vuông cân tại A .

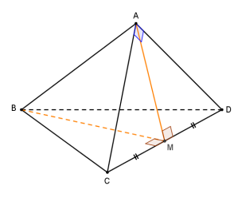
Khi đó, gọi M là trung điểm CD thì: AM $\perp$CD và BM $\perp$CD Ta có:

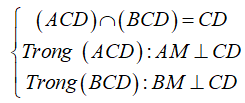
$∆$BCD đều có đường cao

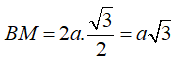
$∆$ACD vuông cân tại A nên trung tuyến

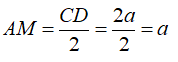
Áp dụng định lý hàm cos trong $∆$AMB, ta có: 

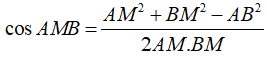
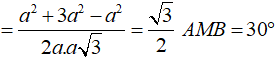
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) có số đo bằng   ${30}^o$