Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải !!
Cho mặt cầu (S) có bán kính R không đổi,...
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kì nội tiếp mặt cầu
Câu hỏi :
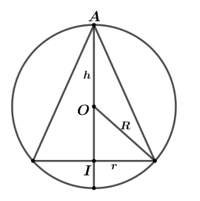
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kì nội tiếp mặt cầu (S) (tham khảo hình vẽ bên). Thể tích khối nón (H) là ; thể tích phần còn lại là . Giá trị lớn nhất của bằng
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Chọn C
Lời giải.
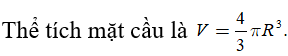
Ta có

Suy ra lớn nhất khi nhỏ nhất => đạt giá trị lớn nhất.
Gọi h,r lần lượt là chiều cao và bán kính đáy của hình nón nội tiếp mặt cầu.
Gọi I, O lần lượt là tâm của đường tròn đáy hình nón và tâm của mặt cầu.
Gọi A là đỉnh của hình nón. Xét thiết diện qua trục của hình nón như hình vẽ bên.
![]()
![]()
Xét hàm
![]()

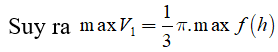

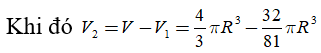
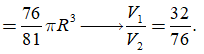
Cách 2.
![]()
TH1. Chiều cao của khối nón h= R + x và bán kính đáy
Theo BĐT Cô si cho 3 số dương, ta có

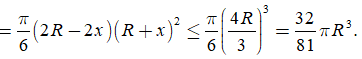
Dấu "=" xảy ra
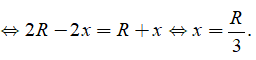
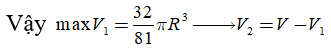
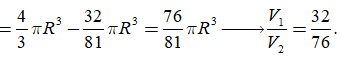
TH2. Chiều cao của khối nón h = R - x. Làm tương tự.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hình học không gian ôn thi THPT Quốc gia có lời giải !!
Số câu hỏi: 181
Copyright © 2021 HOCTAP247
