Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a

* Hướng dẫn giải

Đáp án D

Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó

               2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!

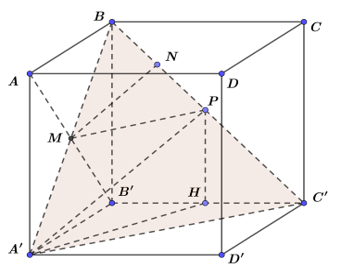
Lời giải: Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là ${30}^0$. Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc ${30}^0$, khi đó MN là đường trung bình của tam giác BA’P nên MN = $\frac{1}{2}$A'P.

Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ =  a – x    (tam giác PC’H vuông cân tại C’), và A'H = 

Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) =  ${30}^0$, do đó

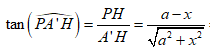
Mặt khác ta lại có A'P = (2)

Từ  (1) và (2) ta tính được 

Từ đây ta rút ra được

=> Chọn phương án D.