Trang chủ
Đề thi & kiểm tra
Vật lý
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Trong giao thoa sóng cơ hai nguồn cùng pha A...
Trong giao thoa sóng cơ hai nguồn cùng pha A và B trên mặt chất lỏng biết AB = 6,6λ. Biết I là trung điểm của AB. Ở mặt chất lỏng, gọi (C) là hình tròn nhận AB là đường kính. M là...
Câu hỏi :
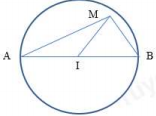
Trong giao thoa sóng cơ hai nguồn cùng pha A và B trên mặt chất lỏng biết AB = 6,6λ. Biết I là trung điểm của AB. Ở mặt chất lỏng, gọi (C) là hình tròn nhận AB là đường kính. M là điểm ở trong (C) xa I nhất dao động với biên độ cực đại và cùng pha với nguồn. Độ dài đoạn MI có giá trị gần nhất với giá trị nào ?
A.
* Đáp án
B
* Hướng dẫn giải
Giả sử phương trình sóng tại hai nguồn là:
Phương trình sóng tại điểm M bất kì trên mặt chất lỏng là:
Để M là điểm dao động cực đại và cùng pha với hai nguồn thì:
Để M là cực đại cùng pha thì: MA − MBvà MA + MB phải cùng là số chẵn hoặc cùng là số lẻ lần bước
sóng ⇒ MA, MB thuộc (1)
|
Chuẩn hóa λ = 1 Vì MI là đường trung tuyến của tam giác AMB nên: (2) Mặt khác vì M nằm trong đường trong đường kính AB nên:
|
 |
Bài toán trở thành tìm cặp số MA, MB thỏa mãn điều kiện (1) sao cho đạt giá trị lớn nhất.
Nhẩm nghiệm ta có cặp thỏa mãn.
Thay vào (2) ta được : MI = 3,1
Chọn B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Số câu hỏi: 1054
Copyright © 2021 HOCTAP247
