Từ các chữ số thuộc tập X = {0;1;2;3;4;5;6;7} có thể lập

* Hướng dẫn giải

Chọn C

Giả sử số lập được có dạng 

Ta có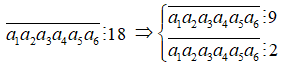 

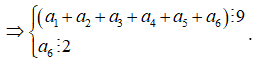
Vì  nên ta có các trường hợp sau

Trường hợp 1: $a_1, a_2, a_3, a_4, a_5, a_6$ được chọn từ 

+ Có 3 cách chọn chọn $a_6$

+ Có 5! cách chọn chọn bộ 5 số 

Suy ra có 3.5! = 360 số.

Trường hợp 2: $a_1, a_2, a_3, a_4, a_5, a_6$  được chọn từ 

+ $a_6$ = 0, có 5! cách chọn bộ 5 số 

+ $a_6$$\ne$0 khi đó $a_6$ có 3 cách chọn, $a_1$ có 4 cách chọn và có 4! cách chọn bộ 4 số 

Suy ra có 5! + 3.4.4!= 408 số

Trường hợp 3: $a_1, a_2, a_3, a_4, a_5, a_6$ được chọn từ 

+ $a_6$ = 0, có 5! cách chọn bộ 5 số 

+ $a_6$$\ne$0 khi đó $a_6$ có 1 cách chọn,  $a_1$ có 4 cách chọn và có 4! cách chọn bộ 4 số 

Suy ra có 5! + 1.4.4! = 216 số

Vậy có: 360 + 408 + 216 = 984 số.