Gọi S là tập hợp các số tự nhiên, mỗi số không có quá 3 chữ số
Câu hỏi :
Gọi S là tập hợp các số tự nhiên, mỗi số không có quá 3 chữ số và tổng các chữ số bằng 9. Lấy ngẫu nhiên một số từ  . Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
. Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
* Đáp án
A
* Hướng dẫn giải
Chọn A
- Bổ đề: Cho ![]() , ta có:
, ta có:
“Số nghiệm nguyên không âm của phương trình ![]()
Thật vậy: Đặt ![]()
Khi đó ![]() và
và ![]()
Hiển nhiên số nghiệm nguyên không âm của (1) bằng số nghiệm nguyên dương của (2)
- Xếp m + n chữ số 1 thành một hàng: có 1 cách.
- Xếp n - 1 dấu gạch ngang "-" vào trong m + n -1 khoảng trống giữa các chữ số 1 (mỗi khoảng trống nhiều nhất một dấu gạch ngang) để chia dãy m + n chữ số 1 thành n phần (mỗi phần có ít nhất một chữ số 1): có cách.
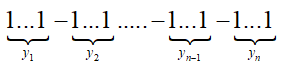
Mỗi phần được chia ra có tổng các chữ số 1 lần lượt là ![]()
và cho ta một nghiệm nguyên dương của phương trình (2).
Do đó số nghiệm nguyên dương của phương trình (2) là ![]()
Suy ra số nghiệm nguyên không âm của phương trình (1) là (đpcm)
Bây giờ ta sẽ áp dụng kết quả của bổ đề để giải bài toán đã cho:
- Tính số phần tử của tập S:
Gọi phần tử của S là vơí ![]() và a + b + c = 9 (*)
và a + b + c = 9 (*)
Theo bổ đề thì số nghiệm nguyên không âm của (*) là ![]()
Vậy n(S) = 55
- Tính số các phần tử của S có chữ số hàng trăm bằng 4.
Khi đó a= 4 và b + c = 5 (**).
Theo bổ đề thì số nghiệm nguyên không âm của (**) là ![]()
Vậy có tất cả 6phần tử của S có chữ số hàng trăm bằng 4.
- Xét phép thử: “Lấy ngẫu nhiên một số từ tập S” và biến cố A: “Số lấy ra có chữ số hàng trăm bằng 4”
Ta có ![]()
Vậy xác suất của biến cố A là 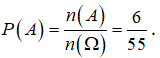
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết !!
Copyright © 2021 HOCTAP247
