Trong một buổi dạ hội có 10 thành viên nam và 12 thành viên nữ

* Hướng dẫn giải

Chọn B

Gọi 2 cặp vợ chồng là C1-V1 và C2-V2 (C=chồng, V=vợ).

* Số cách chọn ra 7 đôi:

- Đầu tiên chọn ra 7 nam trong 10 nam: $C_{10}^7$  (cách).

- Xếp 7 người nam này thành 1 hàng ngang, người đầu tiên có 12 cách ghép với nữ, người thứ hai có 11 cách, cứ như thế suy ra số cách ghép đôi là 12.11.10.9.8.7.6  (cách).

- Theo quy tắc nhân có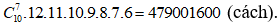 

* Số cách chọn 7 đôi, chỉ có một cặp vợ chồng

- Trường hợp 1: chỉ có cặp vợ chồng C1-V1, khi đó lấy 6 nam trong 9 nam còn lại:

+ Nếu trong 6 nam này không có C2 thì số cách ghép 6 cặp còn lại là:

+ Nếu trong 6 nam này có C2 thì số cách ghép 6 cặp còn lại là: có 10 cách ghép C2 với nữ (trừ  V2 và trừ V1), 5 nam còn lại có  cách, số cách ghép cặp cho 5 nam này là 10.9.8.7.6 cách. Vậy theo quy tắc nhân có

Theo quy tắc cộng, có 

- Trường hợp 2: chỉ có cặp vợ chồng C2-V2, tương tự như trên có 26248320(cách)

Vậy xác suất cần tính là: