Một sóng hình sin lan truyền ở mặt nước từ nguồn O với bước sóng λ. Ba điểm

Phương pháp: 

Phương pháp chuẩn hóa, áp dụng bất đẳng thức cosi 

Bấm máy tính CASIO 

Cách giải:  

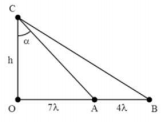
Giữa A và B có 5 đình sóng với A, B cũng là đỉnh sóng ⇒ AB = 4λ 

Chuẩn hóa λ = 1. 

⇒ Từ biểu thức trên, ta thấy rằng góc ACB lớn nhất khi $\mathrm{h}=\sqrt{77}$

+ Gọi M là một điểm trên AC, để M cùng pha với nguồn thì: $\frac{2\pi d_M}{\lambda }=2k\pi \mathrm{ }\Rightarrow d_M=k\lambda$

+ Với khoảng giá trị của d_M tính về phía C từ đường vuông góc của O lên AC: $5,47\le d_M\le 8,7$

Kết hợp với chứ năng Mode 7 ta tìm được k = 6,7,8 

+ Tương tự như vậy ta xét đoạn về phía A: $5,47\le d_M\le 7$

Ta cũng tìm được k = 6,7 

⇒ Trên AC có 5 vị trí dao động cùng pha với nguồn.  

Chọn B.