Trên đường tròn đặt 24 điểm cách đều nhau sao cho độ dài cung
Câu hỏi :
Trên đường tròn đặt 24 điểm cách đều nhau sao cho độ dài cung giữa 2 điểm kề nhau đều bằng 1. Chọn ngẫu nhiên 8 trong 24 điểm đó. Tính xác suất sao cho trong 8 điểm được chọn không có 2 điểm nào có độ dài cung bằng 8 hoặc 3.
* Đáp án
B
* Hướng dẫn giải
Chọn B
Số phần tử không gian mẫu ![]()
Gọi biến cố A = “Chọn 8 điểm sao cho không có 2 điểm nào có độ dài cung bằng 8 hoặc 3”.
Chia 24 điểm của đường tròn thành bảng sau:
|
1 |
9 |
17 |
|
4 |
12 |
20 |
|
7 |
15 |
23 |
|
10 |
18 |
2 |
|
13 |
21 |
5 |
|
16 |
24 |
8 |
|
19 |
3 |
11 |
|
22 |
6 |
14 |
Trong đó, mỗi cột là tập các số có cùng số dư khi chia 3, mỗi hàng là tập các số có cùng số dư khi chia 8. Nhận thấy, mỗi cột không được chọn quá 4 số vì chọn từ 5 số trở lên, sẽ xuất hiện 2 số kề nhau tạo cung có độ dài là 3.
TH1: Chọn 4 số của cột 1 không kề nhau: 2 cách là {1;7;13;19} hoặc {4;10;16;22}
|
1 |
9 |
17 |
|
4 |
12 |
20 |
|
7 |
15 |
23 |
|
10 |
18 |
2 |
|
13 |
21 |
5 |
|
16 |
24 |
8 |
|
19 |
3 |
11 |
|
22 |
6 |
14 |
Tiếp theo, chọn 4 số a,b,c,d còn lại không nằm cùng hàng với 4 số của cột 1 và 2 số bất kỳ trong 4 số a,b,c,d cũng không được cùng hàng với nhau, có cách chọn.
Vậy có 2.= 32cách.
TH2: Chọn 3 số của cột 1 sao cho không có 2 số nào kề nhau: ![]()
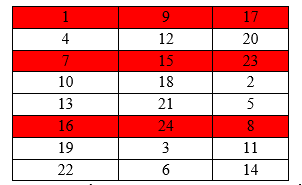
VD chọn{1;7;16} thì 5 số còn lai sẽ thuộc 3 nhóm màu trắng như hình vẽ. Khi đó mỗi nhóm màu trắng trong bảng chỉ có 2 cách chọn. Do đó TH2 có 16.2.2.2=128 cách.
TH3: Chọn 2 số không kề nhau của cột 1: - 8 = 20
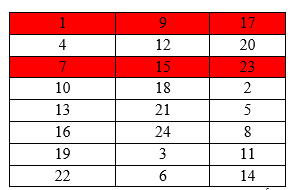
Khi đó, 6 hàng ngang còn lai chia làm 2 nhóm màu trắng như hình vẽ. Mỗi nhóm có đúng 2 cách chọn nên có 20.2.2 = 80 cách.
TH4: Chọn 1 số của cột 1 có 8 cách
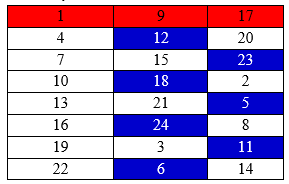
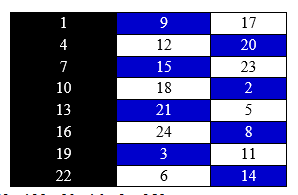
TH5: Chỉ chọn cột 2 với 3. Ta có 2 cách chọn là các dòng xanh hoặc trắng: 2 cách.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết !!
Copyright © 2021 HOCTAP247
