Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi vào hai đầu đoạn mạch AB nối tiếp theo thứ tự cuộn cảm thuần
Câu hỏi :
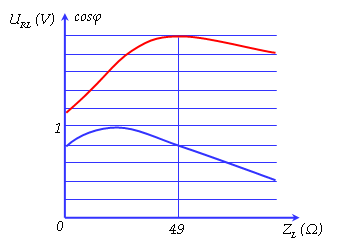
Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi vào hai đầu đoạn mạch AB nối tiếp theo thứ tự cuộn cảm thuần có độ tự cảm thay đổi, điện trở thuần và tụ điện. Gọi ULR là điện áp hiệu dụng đoạn mạch gồm cuộn cảm và điện trở, cosφ là hệ số công suất đoạn mạch AB. Đồ thị bên mô tả sự phụ thuộc của ULR và cosφ theo ZL. Giá trị của R gần nhất với giá trị nào sau đây?

A. 25 Ω.
* Đáp án
D
* Hướng dẫn giải
Phương pháp:
Công thức tính tổng trở: \[Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \]
Hệ số công suất: cosφ = \[\frac{R}{Z}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\]
Cách giải:
Dựa vào đồ thị ta thấy khi ZL = 49 thì URLmax khi đó cosφ = 0,8
URL = \[\frac{U}{Z}.{Z_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\]
URLmax ⇒ \[Z_L^2 - {Z_L}.{Z_C} - {R^2} = 0\]⇒ ZC = 49 -\[\frac{{{R^2}}}{{49}}\]
Hệ số công suất: cosφ = \[\frac{R}{Z}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\]=\[\frac{R}{{\sqrt {{R^2} + {{\left( {49 - (49 - \frac{{{R^2}}}{{49}})} \right)}^2}} }}\]
=\[\frac{R}{{\sqrt {{R^2} + {{\left( {\frac{{{R^2}}}{{49}}} \right)}^2}} }}\]=0,8
⇒ R = 36,75Ω
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
