Trong hiện tượng giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hòa theo phương thẳng đứng
Câu hỏi :
Trong hiện tượng giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hòa theo phương thẳng đứng, cùng pha, cùng tần số 40 Hz. Tốc độ truyền sóng là 1,2 m/s. Ở bề mặt chất lỏng, xét đường tròn tâm A, bán kính AB, điểm nằm trên đường tròn dao động với biên độ cực đại cách đường trung trực của AB một đoạn lớn nhất là b. Giá trị của b gần nhất với giá trị nào sau đây ?
* Đáp án
B
* Hướng dẫn giải
Phương pháp:
Bước sóng:
Điều kiện có cực đại giao thoa:
Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:
Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với kmax.
Sử dụng định lí hàm số cos và các tỉ số lượng giác để tính toán.
Cách giải:
Bước sóng:
Số điểm dao động cực đại trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thỏa mãn:
Để khoảng cách giữa M và đường trung trực max thì M thuộc cực đại ứng với
Mà \[MA = AB = 20cm \Rightarrow MB = 38cm\]
Ta có hình vẽ:
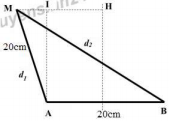
Áp dụng định lí hàm số cos trong tam giác MAB ta có:
\[M{B^2} = M{A^2} + A{B^2} - 2.MA.AB.\cos MAB\]
\[ \Rightarrow MAI = MAB - 900 = {53,6^0}\]
\[ \Rightarrow MI = AB.\sin MAI = 20.0,805 = 16,1cm\]
\[ \Rightarrow b = MH = MI + IH = 16,1 + 10 = 26,1cm\]
Chọn B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
