Tại t1 = 0 đầu O của một sợi dây đàn hồi nằm ngang bắt đầu có một sóng ngang truyền đến và O bắt đầu đi lên
Câu hỏi :
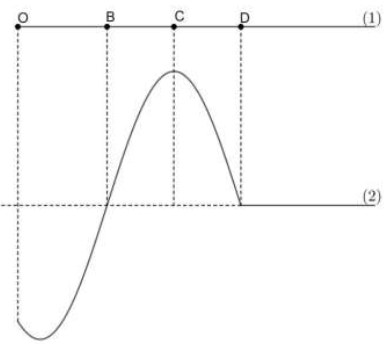
Tại t1 = 0 đầu O của một sợi dây đàn hồi nằm ngang bắt đầu có một sóng ngang truyền đến và O bắt đầu đi lên, các điểm B, C, D trên dây chưa có sóng truyền đến, sợi dây có dạng là đường (1). Tại \[{t_2} = \frac{{5T}}{6}\] (T là chu kỳ sóng) sợi dây có dạng là đường (2). Khoảng cách giữa hai điểm O và C ở thời điểm t2 gấp 1,187 lần khoảng cách giữa O và C ở thời điểm t1. Tỉ số giữa tốc độ truyền sóng trên dây và tốc độ dao động cực đại của mỗi phần tử có giá trị gần nhất là

* Đáp án
C
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị động năng theo thời gian
+ Sử dụng vòng tròn lượng giác.
+ Sử dụng biểu thức tính khoảng cách: \[d = \sqrt {\Delta {d^2} + \Delta {u^2}} \]
+ Sử dụng biểu thức tính tốc độ truyền sóng: v = λ.f
+ Sử dụng biểu thức tính vận tốc dao động cực đại:
Cách giải:
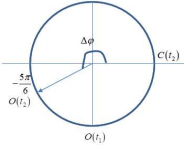
Từ hình ảnh và dữ kiện đề bài ta có vòng tròn lượng giác:
Có:
Độ lệch pha giữa 2 điểm O và C:
Tại thời điểm t1 khoảng cách giữa O và C: \[{d_1} = OC\] (ở trạng thái cân bằng)
Tại thời điểm t2 khoảng cách giữa O và C:
Theo đề bài, ta có:
\[ \Rightarrow \frac{v}{{{v_{\max }}}} = \frac{{\lambda f}}{{\omega a}} = \frac{{\lambda f}}{{2\pi f.a}} = \frac{\lambda }{{2\pi a}} = \frac{5}{{2\pi }} \approx 0,8\]
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
