Trang chủ
Đề thi & kiểm tra
Vật lý
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Trong môi trường đẳng hướng và không hấp thụ âm,...
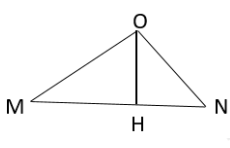
Trong môi trường đẳng hướng và không hấp thụ âm, trên mặt phẳng nằm ngang có 3 điểm O, M, N tạo thành tam giác vuông tại
Câu hỏi :
Trong môi trường đẳng hướng và không hấp thụ âm, trên mặt phẳng nằm ngang có 3 điểm O, M, N tạo thành tam giác vuông tại O, với \(OM = 80\;{\rm{m}},ON = 60\;{\rm{m}}.\) Đặt tại O một nguồn điểm phát âm có công suất P không đổi thì mức cường độ âm tại M là 50 dB. Mức cường độ âm lớn nhất trên đoạn MN gần nhất với giá trị nào sau đây?
A. 54,4dB.
B. 80,2dB.
C. 65,8dB.
D. 52,6 dB.
* Đáp án
A
* Hướng dẫn giải
Phương pháp:
Công thức xác định mức cường độ âm: \(L = 10\log \frac{I}{{{I_0}}}\)
Công thức tính cường độ âm: \(I = \frac{P}{{4\pi {r^2}}}\)
Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
Công thức tính mức cường độ âm trên đoạn MN:
Với r là khoảng cách từ O đến 1 điểm trên MN.
⇒ \({L_{\max }} \Leftrightarrow {r_{\min }} = OH\) (với H là chân đường cao kẻ từ O xuống MN).
Áp dụng hệ thức lượng trong tam giác vuông OMN có:
\(OH = \frac{{OM \cdot ON}}{{MN}} = \frac{{80.60}}{{100}} = 48(\;{\rm{mm}})\)
Lại có:
\( \Rightarrow {L_H} = 50 + 20\log \frac{{OM}}{{OH}} = 50 + 20\log \frac{{80}}{{48}} \approx 54,4dB\)
Chọn A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Số câu hỏi: 1054
Copyright © 2021 HOCTAP247
