Trên đoạn mạch không phân nhánh có bốn điểm theo đúng thứ tự A, M, N, B. Giữa A và M chỉ có điện trở thuần, giữa M và N chỉ có cuộn dây
Câu hỏi :
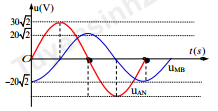
Trên đoạn mạch không phân nhánh có bốn điểm theo đúng thứ tự A, M, N, B. Giữa A và M chỉ có điện trở thuần, giữa M và N chỉ có cuộn dây, giữa N và B chỉ có tụ điện. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có hiệu điện thế hiệu dụng U khi đó công suất tiêu thụ trên đoạn AM bằng công suất tiêu thụ trên đoạn MN. Sự phụ thuộc của hiệu điện thế tức thời hai đầu AN và MB theo thời gian được cho như trên đồ thị. Giá trị của U gần nhất với giá trị nào sau đây?

* Đáp án
C
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị, phân tích mạch điện.
+ Sử dụng phương pháp vẽ giản đồ véc tơ.
+ Công suất tiêu thụ: \(P = \frac{{{U^2} \cdot R}}{{{Z^2}}}\)
+ Áp dụng định lí Pitago trong tam giác vuông.
Cách giải:
+ Mạch điện bao gồm điện trở, cuộn cảm có điện trở, tụ điện.
Nhìn vào đồ thị ta thấy, \[{U_{AN}},{U_{MB}}\] vuông pha vì: \[{U_{AN}}\] cực đại thì UMB cực tiểu và ngược lại.
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{U_{AN}} = 30V}\\{{U_{MB}} = 20V}\\{{U_{AN}} \bot {U_{MB}}}\end{array}} \right.\)
+ Giản đồ véc tơ của mạch điện:
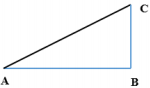
+ Công suất tiêu thụ trên đoạn AM bằng công suất tiêu thụ trên đoạn MN
\( \Rightarrow R = r \Rightarrow {U_R} = {U_r} \Rightarrow AM = MO\)
+ Từ giản đồ véc tơ ta thấy \(\cos NAM = \cos MBN\) (góc có cạnh tương ứng vuông góc, cạnh AO ⊥ AB, cạnh HB ⊥ AN)
\( \Rightarrow \frac{{AO}}{{AN}} = \frac{{OB}}{{MB}} \Rightarrow \frac{{2AM}}{{AN}} = \frac{{\sqrt {M{B^2} - O{M^2}} }}{{MB}} \Leftrightarrow \frac{{2{U_R}}}{{30}} = \frac{{\sqrt {{{20}^2} - U_r^2} }}{{20}} \Rightarrow {U_R} = 12\;{\rm{V}}\)
Áp dụng định lí Pitago trong tam giác vuông AOB có: \(A{B^2} = A{O^2} + O{B^2} \Leftrightarrow {U^2} = \sqrt {{{\left( {2{U_R}} \right)}^2} + {{\left( {{U_{MB}} - {U_r}} \right)}^2}} \)
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
