Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần
Câu hỏi :
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
* Đáp án
C
* Hướng dẫn giải
Phương pháp:
Sử dụng phương pháp giản đồ vecto
Định lí hàm sin: \(\frac{a}{{\sin \hat A}} = \frac{b}{{\sin \hat B}} = \frac{c}{{\sin \hat C}}\)
Gia tốc cực đại của dao động điều hòa: \({a_{\max }} = {\omega ^2}A\)
Cách giải:
Ta có giản đồ vecto:
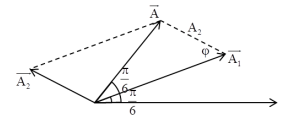
Từ giản đồ vecto, áp dụng định lí hàm sin, ta có:
\(\frac{{{A_2}}}{{\sin \frac{\pi }{6}}} = \frac{A}{{\sin \varphi }} \Rightarrow \frac{A}{{\sin \varphi }} = \frac{4}{{\sin \frac{\pi }{6}}} = 8 \Rightarrow A = 8\sin \varphi \)
Để độ lớn gia tốc của vật đạt giá trị lớn nhất:
\({a_{\max }} \Leftrightarrow {A_{\max }} \Rightarrow {(\sin \varphi )_{\max }} = 1 \Rightarrow {A_{\max }} = 8(\;{\rm{cm}})\)
\( \Rightarrow {a_{\max }} = {\omega ^2}{A_{\max }} = {10^2}.8 = 800\left( {\;{\rm{cm}}/{{\rm{s}}^2}} \right) = 8\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
