Trên mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 14cm, dao động điều hòa cùng tần số, cùng pha, theo
Câu hỏi :
Trên mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 14cm, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. Sóng truyền trên mặt nước với bước sóng 0,9cm. Điểm M nằm trên đoạn AB cách A một đoạn 6cm. Ax, By là hai nửa đường thẳng trên mặt nước, cùng một phía so với AB và vuông góc với AB. Cho điểm C di chuyển trên Ax và điểm D di chuyển trên By sao cho MC luôn vuông góc với MD. Khi diện tích tam giác MCD có giá trị nhỏ nhất thì số điểm dao động với biên độ cực đại trên MD
A. 6.
* Đáp án
C
* Hướng dẫn giải
Phương pháp:
+ Sử dụng biểu thức tính diện tích tam giác: \({S_\Delta } = \frac{1}{2}ab\)
+ Sử dụng BĐT Cosi: \(a + b \ge 2\sqrt {ab} \)
+ Sử dụng điều kiện xảy ra cực đại giao thoa giữa 2 nguồn cùng pha: \({d_2} - {d_1} = k\lambda \)
Cách giải:
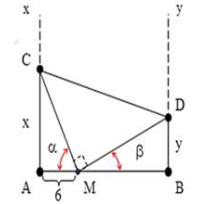
Ta có: \({S_{\Delta M{\rm{D}}}} = {S_{AB{\rm{DC}}}} - {S_{ACM}} - {S_{B{\rm{DM}}}}\)
\( \Rightarrow {S_{\Delta MCD}} = \frac{{(AC + BD)AB}}{2} - \frac{{AC \cdot AM}}{2} - \frac{{DB \cdot BM}}{2}\)
\( \Rightarrow {S_{\Delta MCD}} = \frac{{(x + y) \cdot 14}}{2} - \frac{{x.6}}{2} - \frac{{y.8}}{2} = 4x + 3y\)
Lại có:
\( \Rightarrow \frac{x}{6} = \frac{8}{y} \Rightarrow xy = 48 \Rightarrow 4x.3y = 48.12 = 576\)
Áp dụng BĐT Cosi, ta có:
Dấu “=” xảy ra khi \(4x = 3y\)
Khi đó
Xét tại M, có: \(MB - MA = 8 - 6 = 2\;{\rm{cm}}\)
Xét tại D, có:
Số điểm dao động cực đại trên MD thỏa mãn:
Vậy trên MD có 12 điểm dao động với biên độ cực đại.
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
