Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có
Câu hỏi :
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có \(g = 10\;{\rm{m}}/{{\rm{s}}^2}{\rm{ }}{\rm{. L?y }}{\pi ^2} = 10\). Hình bên là đồ thị biểu diễn sự phụ thuộc của hàm f (t) theo thời gian. (với f (t) là độ lớn của tích lực đàn hồi của lò xo tác dụng lên vật với vận tốc của vật). Biết rằng tại thời điểm ban đầu t = 0, vật đang ở vị trí cân bằng. Độ cứng của lò xo gần nhât với giá trị nào sau đây?
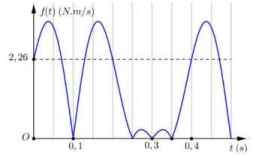

A. 75 N /m
* Đáp án
D
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức tính lực đàn hồi:
+ Vận dụng vòng tròn lượng giác
Cách giải:
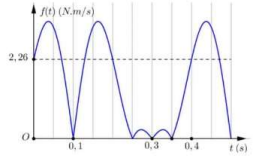
Xét \(f(t) = \left| { - {F_{dh}} \cdot v} \right|\) biểu thức đạt giá trị bằng 0 tại các vị trí biên (v = 0) và vị trí lò xo không bị biến dạng \(\left. {{F_{dh}} = 0 \to x = - \Delta l} \right)\)
Biểu diễn các trạng thái trên đường tròn lượng giác, ta được:
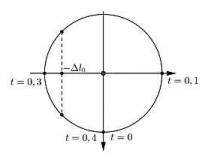
Từ đồ thị và đường tròn ta có:
Chu kì:
\(\Delta l = 4\;{\rm{cm}} = \frac{A}{{\sqrt 2 }} \Rightarrow A = 4\sqrt 2 \;{\rm{cm}}\)
Tại VTCB: \(f(t) = \left| { - {F_{dh}} \cdot {\rm{v}}} \right| = | - k(\Delta l + x) \cdot v|\)
\( \Rightarrow f(t) = k\Delta l.\omega A = 2,26 \Rightarrow k = 63,58\;{\rm{N}}/{\rm{m}}\)
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
