Đặt điện áp xoay chiều (u = U sqrt 2 cos omega { rm{t}} ) (với U và ω không đổi) vào hai
Câu hỏi :
Đặt điện áp xoay chiều \(u = U\sqrt 2 \cos \omega {\rm{t}}\) (với U và ω không đổi) vào hai đầu đoạn mạch AB như hình vẽ. Biết R là biến trở, cuộn cảm thuần có độ tự cảm L, tụ điện có điện dung C thỏa mãn \(LC{\omega ^2} = 2.\) Đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ P của mạch vào R trong trường hợp K mở ứng với đường (1) và trong trường hợp K đóng ứng với đường (2) như hình vẽ. Giá trị của điện trở r bằng
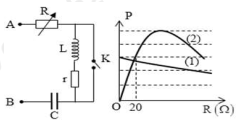

A. 90Ω
* Đáp án
C
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị
+ Khi K đóng mạch gồm RC mắc nối tiếp.
+ Khi K mở mạch gồm RLrC mắc nối tiếp.
+ Vận dụng biểu thức tính công suất:
Cách giải:
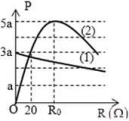
Đặt 1ô theo phương OP có giá trị là a.
Theo đề bài, ta có: \(LC{\omega ^2} = 2 \Leftrightarrow \omega L = \frac{2}{{\omega C}} \Leftrightarrow {Z_L} = 2{{\rm{Z}}_C}\)
+ Khi K đóng: \({P_d} = \frac{{{U^2}}}{{{R^2} + Z_C^2}}R\)
Từ đồ thị, ta thấy \({P_{{d_{{\rm{max }}}}}} = 5{\rm{a}} = \frac{{{U^2}}}{{2{{\rm{R}}_0}}} = \frac{{{U^2}}}{{2{{\rm{Z}}_C}}}{\rm{ (1) }}\)
Và \({P_{{d_{\max }}}}{\rm{ khi }}{R_0} = {Z_C} > 20\Omega \)
Tại \(R = 20\Omega \), ta có: \({P_d} = \frac{{{U^2}}}{{{R^2} + Z_C^2}}R = \frac{{{U^2}}}{{{{20}^2} + Z_C^2}} \cdot 20 = 3{\rm{a}}\left( 2 \right)\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(\frac{5}{3} = \frac{{\frac{1}{{2{Z_C}}}}}{{\frac{{20}}{{{{20}^2} + Z_C^2}}}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{{Z_C} = 60\Omega }\\{{Z_C} = \frac{{20}}{3}\Omega ({\rm{ loai }})}\end{array}} \right.\)
+ Khi K mở: \({P_m} = \frac{{{U^2}}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}(R + r) = \frac{{{U^2}}}{{{{(R + r)}^2} + Z_C^2}}(R + r)\)
Từ đồ thị, ta thấy khi R = 0 thì \({P_m} = 3{\rm{a}} = \frac{{{U^2}}}{{{r^2} + Z_C^2}} \cdot r(3)\)
Lấy \(\frac{{\left( 2 \right)}}{{\left( 3 \right)}}\) ta được: \(\frac{3}{3} = \frac{{\frac{{{U^2}}}{{{{20}^2} + Z_C^2}} \cdot 20}}{{\frac{{{U^2}}}{{{r^2} + Z_C^2}}r}} \Leftrightarrow 1 = \frac{{\frac{{20}}{{{{20}^2} + {{60}^2}}}}}{{\frac{r}{{{r^2} + {{60}^2}}}}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{r = 180\Omega }\\{r = 20\Omega }\end{array}} \right.\)
Do
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
