Có 3 quyển sách toán, 4 quyển sách lí và 5 quyển sách hóa khác
Câu hỏi :
Có 3 quyển sách toán, 4 quyển sách lí và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách gồm có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong ba ngăn (mỗi ngăn đủ rộng để chứa tất cả quyển sách). Tính xác suất để không có bất kì hai quyển sách toán nào đứng cạnh nhau.
* Đáp án
D
* Hướng dẫn giải
Chọn D
Giá có 3 ngăn như vậy có 2 vách ngăn, coi 2 vách ngăn này là 2 quyển sách giống nhau. Khi đó
bài toán trở thành xếp 14 quyển sách (2 quyển “VÁCH NGĂN” giống nhau) vào 14 vị trí. Đầu
tiên chọn 2 vị trị trí xếp vách ngăn là , 12 vị trí còn lại xếp 12 quyển sách là 12!. Vậy không gian mẫu là .12!.
Gọi A là biến cố “không có bất kì hai quyển sách toán nào đứng cạnh nhau”. Ta tìm số cách xếp thỏa mãn A
Đầu tiên ta xếp 11 quyển sách gồm 4 quyển lí, 5 quyển hóa và 2 quyển “VÁCH NGĂN”. Cũng
như trên, ta chọn 2 vị trí xếp 2 quyển “VÁCH NGĂN” trước là sau đó xếp 9 quyển còn lại là 9!. Vậy số cách xếp 11 quyển này là .9!. Sau khi xếp xong 11 quyển này thì sẽ có sẽ có 12 khe. Ta chọn 3 khe để xếp 3 quyển toán còn lại, là .
Vậy số cách thỏa mãn biến cố A là ..9!.
Vậy 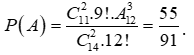 .
.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết !!
Copyright © 2021 HOCTAP247
