Trang chủ
Đề thi & kiểm tra
Vật lý
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Hình bên là một đoạn đồ thị biểu diễn sự...
Hình bên là một đoạn đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa. Phương trình
Câu hỏi :
Hình bên là một đoạn đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa. Phương trình dao động của vật là
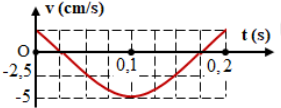

A. \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t + \frac{\pi }{6}} \right)cm\)
B. \(x = \frac{3}{{8\pi }}\cos \left( {\frac{{20\pi }}{3} + \frac{\pi }{6}} \right)cm\)
C. \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)cm\)
D. \(x = \frac{3}{{8\pi }}\cos \left( {\frac{{20\pi }}{3} - \frac{\pi }{6}} \right)cm\)
* Đáp án
C
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị v – t
+ Sử dụng vòng tròn lượng giác.
+ Sử dụng công thức góc quét:
+ Sử dụng biểu thức tính vận tốc cực đại: \({v_{\max }} = A\omega \)
+ Sử dụng biểu thức: \({\varphi _v} - {\varphi _x} = \frac{\pi }{2}\)
Cách giải:
Từ đồ thị, ta có:
+ Vận tốc cực đại: \({v_{max}} = 5\;{\rm{cm}}/s\)
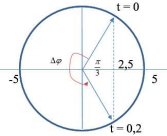
Vòng tròn lượng giác:
Từ vòng tròn lượng giác ta có:
Mặt khác:
Lại có:
Tại thời điểm ban đầu :
⇒ Phương trình li độ: \(x = \frac{3}{{4\pi }}\cos \left( {\frac{{20\pi }}{3}t - \frac{\pi }{6}} \right)cm\)
Chọn C.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Số câu hỏi: 1054
Copyright © 2021 HOCTAP247
