Một mạch dao động LC lí tưởng có (C = {2.10^{ - 9}}F ) đang dao động điện từ tự do. Cường độ dòng điện tức thời trong
Câu hỏi :
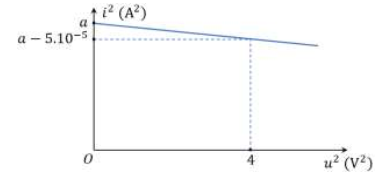
Một mạch dao động LC lí tưởng có \(C = {2.10^{ - 9}}F\) đang dao động điện từ tự do. Cường độ dòng điện tức thời trong mạch và hiệu điện thế tức thời giữa hai bản tụ điện lần lượt là i và u. Sự phụ thuộc của \({i^2}\) vào \({u^2}\) được biểu diễn bằng một đoạn đồ thị như hình vẽ. Giá trị của L là

* Đáp án
A
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)
+ Sử dụng biểu thức: \(\frac{{CU_0^2}}{2} = \frac{{LI_0^2}}{2}\)
Cách giải:
Trong mạch LC ta có: \(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)
Từ đồ thị, ta có:
+ Tại \({u^2} = 0\) thì \({i^2} = a \Rightarrow I_0^2 = a\)
+ Tại \({u^2} = 4\) thì \({i^2} = a - {5.10^{ - 5}}\) ta suy ra: \(\frac{{a - 5 \cdot {{10}^{ - 5}}}}{{I_0^2}} + \frac{4}{{U_0^2}} = 1 \Leftrightarrow \frac{{a - 5 \cdot {{10}^{ - 5}}}}{a} + \frac{4}{{U_0^2}} = 1 \Rightarrow U_0^2 = 80000{\rm{a}}\)
Lại có:
\(I_0^2 = \frac{C}{L}U_0^2 \Leftrightarrow a = \frac{{{{2.10}^{ - 9}}}}{L} \cdot 80000a \Rightarrow L = {1,6.10^{ - 4}}H = 0,16mH\)
Chọn A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
