Trang chủ
Đề thi & kiểm tra
Vật lý
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Đặt điện áp (u = 180 sqrt 2 cos omega...
Đặt điện áp (u = 180 sqrt 2 cos omega { rm{t}}({ rm{V}}) ) (với ω không đổi) vào hai đầu đoạn mạch AB gồm đoạn
Câu hỏi :
Đặt điện áp \(u = 180\sqrt 2 \cos \omega {\rm{t}}({\rm{V}})\) (với ω không đổi) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắc nối tiếp với đoạn mạch MB. Đoạn mạch AM chỉ có điện trở thuần R đoạn mạch MB gồm tụ điện có điện dung C mắc nối tiếp với cuộn cảm thuần có độ tự cảm L thay đổi được. Điều chỉnh giá trị L và thấy rằng: khi điện áp u và cường độ dòng điện trong mạch lệch pha nhau \({\varphi _1}\) thì điện áp hiệu dụng ở hai đầu đoạn mạch AM là U, khi điện áp u và cường độ dòng điện trong mạch lệch pha nhau \({\varphi _2}\) thì điện áp hiệu dụng ở hai đầu đoạn mạch AM là \(\sqrt 3 U\). Biết \({\varphi _1} + {\varphi _2} = {90^0}\). Giá trị của U là
A. 180 V.
B. 135 V.
C. 60 V.
D. 90V.
* Đáp án
D
* Hướng dẫn giải
Phương pháp:
+ Vận dụng pha dao động trong đoạn mạch xoay chiều
+ Sử dụng giản đồ véctơ quay.
+ Sử dụng hệ thức lượng trong tam giác.
Cách giải:
Do U hai đầu đoạn mạch không đổi và \({u_R} \bot {u_{LC}}\)
⇒Khi L thay đổi thì tập hợp các điểm M là đường tròn đường kính là hiệu điện thế giữa hai đầu đoạn mạch U =180 V
Mặt khác, độ lệch pha giữa u và I cũng là độ lệch pha giữa
Từ đó, ta có giản đồ véctơ điện áp như hình vẽ:
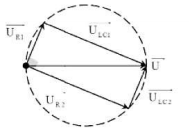
Từ giản đồ ta suy ra \({u_{{R_1}}} \bot {u_{{R_2}}} \Rightarrow U_{{R_1}}^2 + U_{{R_2}}^2 = U_{AB}^2 \Leftrightarrow {U^2} + 3{U^2} = {180^2} \Rightarrow U = 90\;{\rm{V}}\)
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Số câu hỏi: 1054
Copyright © 2021 HOCTAP247
