Trong một đoạn mạch điện xoay chiều RLC, công suất tức thời p thay đổi theo thời gian t. Hình bên là đồ thị biểu diễn sự
Câu hỏi :
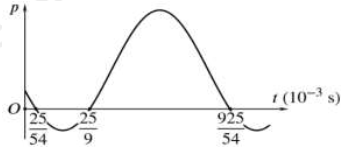
Trong một đoạn mạch điện xoay chiều RLC, công suất tức thời p thay đổi theo thời gian t. Hình bên là đồ thị biểu diễn sự phụ thuộc của p vào t. Hệ số công suất của mạch là

* Đáp án
D
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị p-t
+ Sử dung biểu thức tính công suất tức thời: p = ui
+ Sử dụng phương trình lượng giác.
Cách giải:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{u = {U_0}\cos \left( {\omega t + {\varphi _u}} \right)}\\{i = {I_0}\cos \left( {\omega t + {\varphi _i}} \right)}\end{array}} \right.\)
Đặt: \(\left\{ {\begin{array}{*{20}{l}}{{\varphi _u} + {\varphi _i} = x}\\{{\varphi _u} - {\varphi _i} = \varphi }\end{array}} \right.\)
Công suất tức thời: \(p = ui = UI.[\cos (2\omega t + x) + \cos \varphi ]\)
Từ đồ thị, ta thấy:
Công suất:
Tại
\( \Leftrightarrow \cos \left( {2\omega {t_1} + x} \right) = \cos \left( {2\omega {t_2} + x} \right) \Leftrightarrow \cos \left( {2.120\pi \frac{{{{25.10}^{ - 3}}}}{{54}} + x} \right) = \cos \left( {2.120\pi \frac{{25}}{9} \cdot {{10}^{ - 3}} + x} \right)\)
Thay vào (1) ta suy ra:
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
