Một con lắc lò xo dao động điều hòa theo phương thẳng đứng dọc theo trục tọa độ Ox, chiều dương hướng xuống, gốc
Câu hỏi :
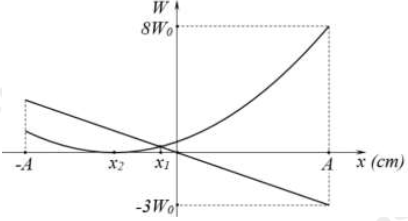
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng dọc theo trục tọa độ Ox, chiều dương hướng xuống, gốc O tại vị trí cân bằng của vật nhỏ. Chọn mốc thế năng trọng trường ở vị trí cân bằng của vật nhỏ. Hình vẽ bên là các đồ thị biểu diễn sự phụ thuộc của thế năng trọng trường và thế năng đàn hồi vào li độ x của dao động. Trong đó hiệu \({x_1} - {x_2} = 3,66cm\). Biên độ dao động A của con lắc lò xo có giá trị bằng

* Đáp án
B
* Hướng dẫn giải
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức tính độ dãn của lò xo tại \({\rm{VTCB}}:\Delta l = \frac{{mg}}{k}\)
+ Sử dụng biểu thức tính thế năng đàn hồi: \({{\rm{W}}_{dh}} = \frac{1}{2}k\Delta {l^2}\) với\({\rm{ }}\Delta l\)là độ biến dạng của lò xo
+ Sử dụng biểu thức tính thế năng trọng trường:
Cách giải:
Từ đồ thị, ta thấy thế năng đàn hồi cực tiểu = 0 tại x2 \( \Rightarrow \) đây chính là độ dãn của lò xo tại VTCB
Lại có:
+ Thế năng đàn hồi: \({{\rm{W}}_{{\rm{d}}h}} = \frac{1}{2}k{\left( {x - {x_2}} \right)^2}\)
+ Thế năng trọng trường:
Từ đồ thị:
+ Xét tại
Theo đề bài ta có: \({x_1} - {x_2} = 3,66\;{\rm{cm}} \Rightarrow \) thay vào (*) ta suy ra:
+ Xét tại
Thay số vào ta suy ra:\(\frac{8}{{ - 3}} = \frac{{{{(A + 4,9997)}^2}}}{{2 \cdot A( - 4,9997)}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{A = 14,9991\;{\rm{cm}}}\\{A = 1,667\;{\rm{cm}}}\end{array}} \right.\)
Chọn B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!
Copyright © 2021 HOCTAP247
