Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng \(a\sqrt 2 \), \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\sqrt 3 \)

* Hướng dẫn giải

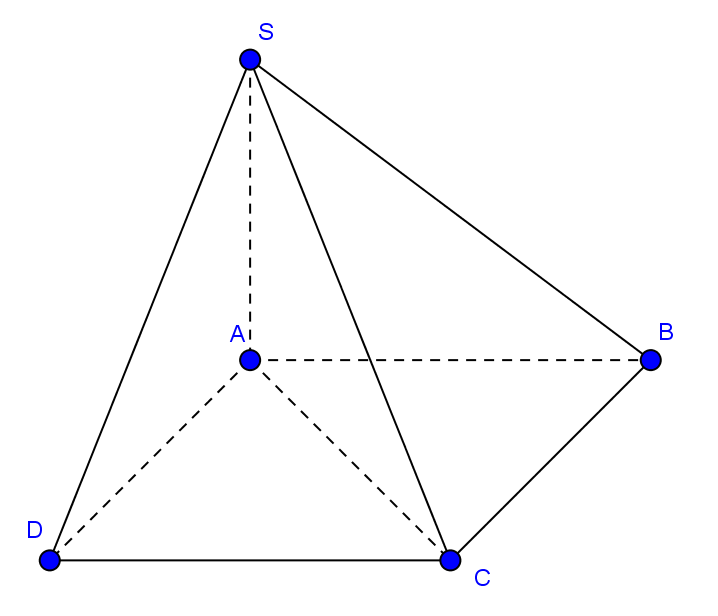
a) Ta có: \(\left\{ \begin{array}{l}
BD \bot AC\,\,\left( {ABCD\left( {hv} \right)} \right)\\
BD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\
SA \cap AC = A
\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)

b) Vì AC là hình chiếu của SC trên mặt phẳng (ABCD) nên góc giữa SC và mp (ABCD) là góc SCA

Ta có: \(AC = a\sqrt 2 .\sqrt 2  = 2a \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \sqrt 3  \Rightarrow \widehat {SAC} = {60^0}\)