Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) !!
Cho tứ diện ABCD có AB = AC = AD...
Cho tứ diện ABCD có AB = AC = AD và góc BAC = góc BAD = 60 độ, góc CAD = 90 độ
Câu hỏi :
Cho tứ diện ABCD có AB = AC = AD và , . Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ và ?
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Chọn B
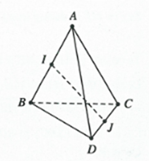
Xét tam giác ICD có J là trung điểm CD
Tam giác ABC có đều
Tương tự ta có đều nên
Ta có
.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) !!
Số câu hỏi: 499
Copyright © 2021 HOCTAP247
