Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tâm

* Hướng dẫn giải

a)

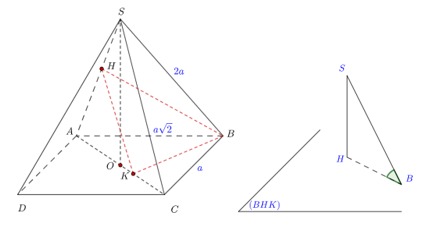
+ Xét tam giác SAC có SA = SC = 2a nên tam giác SAC cân tại S, có O là trung điểm của AC nên SO là đường trung tuyến và cũng là đường cao của tam giác SAC

Suy ra SO ^ AC (1)

+ Xét tam giác SAC có SB = SD = 2a nên tam giác SBD cân tại S, có O là trung điểm của BD nên SO là đường trung tuyến và cũng là đường cao của tam giác SBD

Suy ra SO ^ BD (2)

Từ (1) và (2) nên ta có SO ^ (ABCD)

b) Ta có:

Từ đó suy ra BK ^ SH

Mà KH ^ SH

Nên ta có SH ^ (BKH) Þ (SB, (BKH)) = (SB, HB) = a

Ta cũng suy ra được SH ^ BH

$$\begin{gathered} \cos \widehat{SBA}=\frac{S{B}^2+B{A}^2-S{A}^2}{2.SB.BA} \\ =\frac{{\left(2a\right)}^2+{\left(a\sqrt{2}\right)}^2-{\left(2a\right)}^2}{2.2a.a\sqrt{2}}=\frac{\sqrt{2}}{4} \\ \Rightarrow \sin \widehat{SBA}=\sqrt{1-{\left(\cos \widehat{SBA}\right)}^2}=\frac{\sqrt{14}}{4} \end{gathered}$$

Ta có:

$$\begin{gathered} S_{SAB}=\frac{1}{2}SB.AB.\sin \widehat{SBA}=\frac{1}{2}HB.AS \\ \Rightarrow HB=\frac{SB.AB.\sin \widehat{SBA}}{SA} \\ =\frac{2a.a\sqrt{2}.\frac{\sqrt{14}}{4}}{2a}=\frac{a\sqrt{7}}{2} \\ \cos \alpha =\frac{HB}{SB}=\frac{\frac{a\sqrt{7}}{2}}{2a}=\frac{\sqrt{7}}{4}. \end{gathered}$$