Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi M là

Đáp án đúng là: A

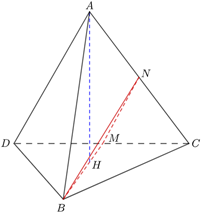
Kẻ MN // AD (M Î CD).

Góc giữa hai đường thẳng AD và BM là góc giữa hai đường thẳng MN và BM và là góc a.

Vì M là trung điểm của CD.

Nên BM là đường trung tuyến của tam giác đều BCD cạnh a.

Do đó .$BM=\frac{a\sqrt{3}}{2}$

Vì M là trung điểm của CD và MN // AD nên N cũng là trung điểm của AC.

Suy ra BN là đường trung tuyến của tam giác đều BCA cạnh a.

Do đó $BN=\frac{a\sqrt{3}}{2}$ .

Vì M, N lần lượt là trung điểm của CD và AC nên MN là đường trung bình của tam giác ACD.

Suy ra$MN=\frac{1}{2}AD=\frac{a}{2}$

.$$\begin{gathered} \cos \widehat{BMN}=\frac{B{M}^2+M{N}^2-B{N}^2}{2.BM.MN} \\ =\frac{{\left(\frac{a\sqrt{3}}{2}\right)}^2+{\left(\frac{a}{2}\right)}^2-{\left(\frac{a\sqrt{3}}{2}\right)}^2}{2.\frac{a\sqrt{3}}{2}.\frac{a}{2}} \end{gathered}$$

Do đó$cos\alpha =\frac{\sqrt{3}}{6}.$

Vậy cosin của góc giữa hai đường thẳng AD và BM là$\frac{\sqrt{3}}{6}.$