Cho hình bình hành ABCD. Gọi Ax, By,Cz,Dt lần lượt là các đường thẳng

* Hướng dẫn giải

Đáp án C

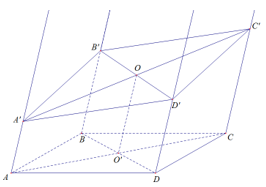
Trên Ax lấy điểm A’ sao cho AA’= x

Trên By lấy điểm B’ sao cho BB’ = y

Trên Cz lấy điểm C’ sao cho CC’ = z

Hai mp (AA'B'B) // ( DD'C'C) vì AA'// DD'  và AB// DC

Mặt phẳng (P) cắt 2 mp song song (AA'B'B)và (DD'C'C) theo 2 giao tuyến là A'B'và C'D'

Suy ra: A'B' // C'D' ( định lí giao tuyến).

 Gọi $\left\{O\text{'}\right\}=AC\cap BD,\left\{O\right\}=A\text{'}C\text{'}\cap B\text{'}D\text{'}$

Xét hình thang AA’C’C có: OO’ là đường trung bình

 $\Rightarrow OO\text{'}=\frac{AA\text{'}+CC\text{'}}{2}=\frac{x+z}{2}$ (1)

Xét tam giác BDD’D có: OO’ là đường trung bình

$\Rightarrow OO\text{'}=\frac{DD\text{'}+BB\text{'}}{2} = \frac{DD\text{'} +\hspace{0.17em}y}{2}$  (2)

 Từ (1) và (2) suy ra:  x + z =DD' +y 

Nên: DD’ = x + z – y