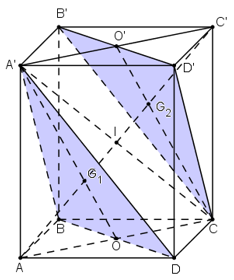
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C)

* Hướng dẫn giải

a) + A’D’ // BC và A’D’ = BC

⇒ A’D’CB là hình bình hành

⇒ A’B // D’C, mà D’C ⊂ (B’D’C) ⇒ A’B // (B’D’C) (1)

+ BB’ // DD’ và BB’ = DD’

⇒ BDD’B’ là hình bình hành

⇒ BD // B’D’, mà B’D’ ⊂ (B’D’C) ⇒ BD // (B’D’C) (2)

A’B ⊂ (BDA’) và BD ⊂ (BDA’); A’B ∩ BD = B (3)

Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C).

b) Gọi O = AC ∩ BD

+ Ta có: O ∈ AC ⊂ (AA’C’C)

⇒ A’O ⊂ (AA’C’C).

Trong (AA’C’C), gọi A’O ∩ AC’ = G1.

G1 ∈ A’O ⊂ (A’BD)

⇒ G1 ∈ AC’ ∩ (BDA’).

+ Trong hình bình hành AA’C’C gọi I = A’C ∩ AC’

⇒ A’I = IC.

⇒ AI là trung tuyến của ΔA’AC

$\Rightarrow G_{1 }= A’O \cap AC’$ là giao của hai trung tuyến AI và A’O của ΔA’AC

$\Rightarrow G_1$ là trọng tâm ΔA’AC

$\Rightarrow A’G_1 = 2.A’O/3$

$\Rightarrow G_1$ cũng là trọng tâm ΔA’BD.

Vậy AC' đi qua trọng tâm $G_1$ của ΔA’BD.

Chứng minh tương tự đối với điểm $G_2$.

c) *Vì $G_1$ là trọng tâm của ΔAA’C nên $A{G}_1/AI = 2/3$ .

Vì I là trung điểm của AC’ nên AI = 1/2.AC’

Từ các kết quả này, ta có : $A{G}_1 = 1/3.AC’$

*Chứng minh tương tự ta có : $C’G_2 = 1/3.AC’$

Suy ra : $A{G}_1 = G_1{G}_2 = G_{2}C’ = 1/3.AC’$.

d) (A’IO) chính là mp (AA’C’C) nên thiết diện cần tìm chính là hình bình hành AA’C’C.