Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Giải toán 11: Hình học !!
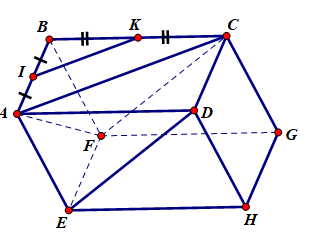
Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt...
Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC
Câu hỏi :
Cho hình hộp ABCD.EFGH. Gọi I và K lần lượt là trung điểm của các cạnh AB và BC. Chứng minh rằng các đường thẳng IK và ED song song với mặt phẳng (AFC). Từ đó suy ra ba vecto đồng phẳng.
* Đáp án
* Hướng dẫn giải
I và K lần lượt là trung điểm của các cạnh AB và BC ⇒ IK là đường trung bình của ∆ABC nên IK // AC ⊂ (AFC) ⇒ IK // (AFC)
hình hộp ABCD.EFGH nên các mặt của hình hộp là hình bình hành.
Suy ra: EF// CD(cùng // GH) và EF = CD ( cùng = GH)
EFCD là hình bình hành
⇒ ED // CF
Nên ED // (AFC)
⇒ ba vecto đồng phẳng (vì giá của chúng song song với một mặt phẳng)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 11: Hình học !!
Số câu hỏi: 209
Copyright © 2021 HOCTAP247