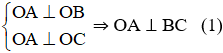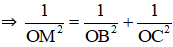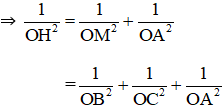Trang chủ
Đề thi & kiểm tra
Lớp 11
Toán học
Giải toán 11: Hình học !!
Cho tứ diện OABC có ba cạnh OA, OB và...
Cho tứ diện OABC có ba cạnh OA, OB và OC đôi một vuông góc
Câu hỏi :
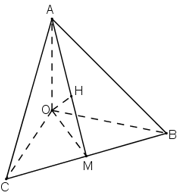
Cho tứ diện OABC có ba cạnh OA, OB và OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng
* Đáp án
* Hướng dẫn giải
a) Ta có:
Do H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC) nên:
OH ⊥ (ABC) ⇒ OH ⊥ BC (2)
Mà OA; OH ⊂ (OAH); OA ∩ OH = O (3)
Từ (1); (2) và (3) ⇒ BC ⊥ (OAH)
⇒ BC ⊥ AH
Chứng minh tương tự ta có: AC ⊥ BH
⇒ H là trực tâm ΔABC.
b) Gọi M = AH ∩ BC.
+ BC ⊥ (OAH) ⇒ BC ⊥ OM.
ΔOBC vuông tại O có đường cao OM
+ OA ⊥ (OBC) ⇒ OA ⊥ OM ⇒ ΔOAM vuông tại O.
OH ⊥ (ABC) ⇒ OH ⊥ AM.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 11: Hình học !!
Số câu hỏi: 209
Copyright © 2021 HOCTAP247